Characterization of coherent structures in the cardiovascular system
- PMID: 18437573
- PMCID: PMC3886852
- DOI: 10.1007/s10439-008-9502-3
Characterization of coherent structures in the cardiovascular system
Abstract
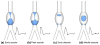
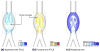
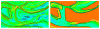
Recent advances in blood flow modeling have provided highly resolved, four-dimensional data of fluid mechanics in large vessels. The motivation for such modeling is often to better understand how flow conditions relate to health and disease, or to evaluate interventions that affect, or are affected by, blood flow mechanics. Vessel geometry and the pulsatile pumping of blood leads to complex flow, which is often difficult to characterize. This article discusses a computational method to better characterize blood flow kinematics. In particular, we compute Lagrangian coherent structures (LCS) to study flow in large vessels. We demonstrate that LCS can be used to characterize flow stagnation, flow separation, partitioning of fluid to downstream vasculature, and mechanisms governing stirring and mixing in vascular models. This perspective allows valuable understanding of flow features in large vessels beyond methods traditionally considered.
Figures




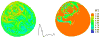


Similar articles
-
A flow quantification method using fluid dynamics regularization and MR tagging.IEEE Trans Biomed Eng. 2010 Jun;57(6):1437-45. doi: 10.1109/TBME.2009.2038229. Epub 2010 Feb 17. IEEE Trans Biomed Eng. 2010. PMID: 20172815
-
Characterization of Hemodynamics in Great Arteries of Wild-Type Mouse Using Computational Fluid Dynamics Based on Ultrasound Images.Ultrasound Q. 2016 Mar;32(1):51-7. doi: 10.1097/RUQ.0000000000000164. Ultrasound Q. 2016. PMID: 26938034
-
Efficient blood flow visualization using flowline extraction and opacity modulation based on vascular structure analysis.Comput Biol Med. 2017 Mar 1;82:87-99. doi: 10.1016/j.compbiomed.2017.01.020. Epub 2017 Jan 31. Comput Biol Med. 2017. PMID: 28167407
-
Blood cell interactions and segregation in flow.Ann Biomed Eng. 2008 Apr;36(4):534-44. doi: 10.1007/s10439-007-9429-0. Epub 2008 Jan 11. Ann Biomed Eng. 2008. PMID: 18188702 Free PMC article. Review.
-
Red blood cell flow in the cardiovascular system: a fluid dynamics perspective.Crit Rev Biomed Eng. 2012;40(5):427-40. doi: 10.1615/critrevbiomedeng.v40.i5.30. Crit Rev Biomed Eng. 2012. PMID: 23339650 Review.
Cited by
-
Characterization of the transport topology in patient-specific abdominal aortic aneurysm models.Phys Fluids (1994). 2012 Aug;24(8):81901. doi: 10.1063/1.4744984. Epub 2012 Aug 10. Phys Fluids (1994). 2012. PMID: 22952409 Free PMC article.
-
Impact of poroelasticity of intraluminal thrombus on wall stress of abdominal aortic aneurysms.Biomed Eng Online. 2012 Aug 29;11:62. doi: 10.1186/1475-925X-11-62. Biomed Eng Online. 2012. PMID: 22931215 Free PMC article.
-
Detecting dynamical boundaries from kinematic data in biomechanics.Chaos. 2010 Mar;20(1):017507. doi: 10.1063/1.3267043. Chaos. 2010. PMID: 20370297 Free PMC article.
-
A novel multiblock immersed boundary method for large eddy simulation of complex arterial hemodynamics.J Comput Phys. 2013 Dec 1;254:10.1016/j.jcp.2013.07.033. doi: 10.1016/j.jcp.2013.07.033. J Comput Phys. 2013. PMID: 24179251 Free PMC article.
-
Effect of exercise on patient specific abdominal aortic aneurysm flow topology and mixing.Int J Numer Method Biomed Eng. 2014 Feb;30(2):280-95. doi: 10.1002/cnm.2601. Epub 2013 Oct 28. Int J Numer Method Biomed Eng. 2014. PMID: 24493404 Free PMC article.
References
-
- Adrian RJ. Particle imaging techniques for experimental fluid mechanics. Annu Rev Fluid Mech. 1991;23:261–304.
-
- Bharadvaj BK, Mabon RF, Giddens DP. Steady flow in a model of the human carotid bifurcation. Part I—Flow visualization. J Biomech. 1982;15(5):349–362. - PubMed
-
- Bluestein D, Niu L, Schoephoerster RT, Dewanjee MK. Steady flow in an aneurysm model: correlation between fluid dynamics and blood platelet deposition. J Biomech Eng. 1996;118(3):280–294. - PubMed
-
- Egelhoff CJ, Budwig RS, Elger DF, Khraishi TA, Johansen KH. Model studies of the flow in abdominal aortic aneurysms during resting and exercise conditions. J Biomech. 1999;32(12):1319–1329. - PubMed
-
- Fehlberg E. Low-order classical Runge-Kutta formulas with step size control and their application to some heat transfer problems. NASA Technical Report. 1969;315
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

