Cooperativity and specificity in enzyme kinetics: a single-molecule time-based perspective
- PMID: 18441030
- PMCID: PMC2426636
- DOI: 10.1529/biophysj.108.131771
Cooperativity and specificity in enzyme kinetics: a single-molecule time-based perspective
Abstract
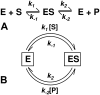
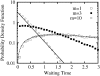
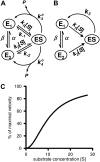
An alternative theoretical approach to enzyme kinetics that is particularly applicable to single-molecule enzymology is presented. The theory, originated by Van Slyke and Cullen in 1914, develops enzyme kinetics from a "time perspective" rather than the traditional "rate perspective" and emphasizes the nonequilibrium steady-state nature of enzymatic reactions and the significance of small copy numbers of enzyme molecules in living cells. Sigmoidal cooperative substrate binding to slowly fluctuating, monomeric enzymes is shown to arise from association pathways with very small probability but extremely long passage time, which would be disregarded in the traditional rate perspective: A single enzyme stochastically takes alternative pathways in serial order rather than different pathways in parallel. The theory unifies dynamic cooperativity and Hopfield-Ninio's kinetic proofreading mechanism for specificity amplification.
Figures

Similar articles
-
Emergence of dynamic cooperativity in the stochastic kinetics of fluctuating enzymes.J Chem Phys. 2016 Aug 28;145(8):085103. doi: 10.1063/1.4961540. J Chem Phys. 2016. PMID: 27586952
-
Open-system nonequilibrium steady state: statistical thermodynamics, fluctuations, and chemical oscillations.J Phys Chem B. 2006 Aug 10;110(31):15063-74. doi: 10.1021/jp061858z. J Phys Chem B. 2006. PMID: 16884217
-
Complex kinetics of fluctuating enzymes: phase diagram characterization of a minimal kinetic scheme.Chem Asian J. 2010 May 3;5(5):1129-38. doi: 10.1002/asia.200900627. Chem Asian J. 2010. PMID: 20235274
-
Practical steady-state enzyme kinetics.Methods Enzymol. 2014;536:3-15. doi: 10.1016/B978-0-12-420070-8.00001-5. Methods Enzymol. 2014. PMID: 24423262 Review.
-
Multiple alternative substrate kinetics.Biochim Biophys Acta. 2015 Nov;1854(11):1729-36. doi: 10.1016/j.bbapap.2015.05.016. Epub 2015 Jun 4. Biochim Biophys Acta. 2015. PMID: 26051088 Review.
Cited by
-
Michaelis-Menten relations for complex enzymatic networks.J Chem Phys. 2011 Apr 21;134(15):155101. doi: 10.1063/1.3580564. J Chem Phys. 2011. PMID: 21513417 Free PMC article.
-
Statistics and Related Topics in Single-Molecule Biophysics.Annu Rev Stat Appl. 2014 Jan 1;1:465-492. doi: 10.1146/annurev-statistics-022513-115535. Annu Rev Stat Appl. 2014. PMID: 25009825 Free PMC article.
-
The chemical master equation approach to nonequilibrium steady-state of open biochemical systems: linear single-molecule enzyme kinetics and nonlinear biochemical reaction networks.Int J Mol Sci. 2010 Sep 20;11(9):3472-500. doi: 10.3390/ijms11093472. Int J Mol Sci. 2010. PMID: 20957107 Free PMC article. Review.
-
Dynamics and Location of the Allosteric Midazolam Site in Cytochrome P4503A4 in Lipid Nanodiscs.Biochemistry. 2020 Feb 18;59(6):766-779. doi: 10.1021/acs.biochem.9b01001. Epub 2020 Jan 27. Biochemistry. 2020. PMID: 31961139 Free PMC article.
-
Application of the principles of systems biology and Wiener's cybernetics for analysis of regulation of energy fluxes in muscle cells in vivo.Int J Mol Sci. 2010 Mar 8;11(3):982-1019. doi: 10.3390/ijms11030982. Int J Mol Sci. 2010. PMID: 20479996 Free PMC article. Review.
References
-
- Beard, D. A., and H. Qian. 2008. Chemical biophysics: quantitative analysis of cellular systems. In Cambridge Texts in Biomedical Engineering. Cambridge University Press, New York.
-
- Cornish-Bowden, A. 2004. Fundamentals of Enzyme Kinetics. Portland Press, London, UK.
-
- English, B. P., W. Min, A. M. van Oijen, K. T. Lee, G. Luo, H. Sun, B. J. Cherayil, S. C. Kou, and X. S. Xie. 2006. Ever-fluctuating single enzyme molecules: Michaelis-Menten equation revisited. Nat. Chem. Biol. 2:87–94. - PubMed
-
- Qian, H. 2002. Equations for stochastic macromolecular mechanics of single proteins: equilibrium fluctuations, transient kinetics and nonequilibrium steady-state. J. Phys. Chem. B. 106:2065–2073.
MeSH terms
Substances
LinkOut - more resources
Full Text Sources

