Diffusive coupling and network periodicity: a computational study

Abstract

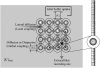
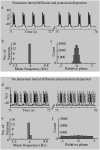
Diffusive coupling (nearest-neighbor coupling) is the most common type of coupling present in many systems. Previous experimental and theoretical studies have shown that potassium lateral diffusion coupling (i.e., diffusive coupling) can be responsible for synchronization of neuronal activity. Recent in vivo experiments carried out with anesthetized rat hippocampus suggested that the extracellular potassium could play an important role in the generation of a novel type of epileptiform nonsynaptic activity. Yet, the role of potassium in the generation of seizures remains controversial. We tested the hypothesis that potassium lateral diffusion coupling is responsible for the coupling mechanisms for network periodicity in a nonsynaptic model of epilepsy in vivo using a CA1 pyramidal neuron network model The simulation results show that 1), potassium lateral diffusion coupling is crucial for establishing epileptiform activity similar to that generated experimentally; and 2), there exists a scaling relation between the critical coupling strength and the number of cells in the network. The results not only agree with the theoretical prediction, but strongly suggest that potassium lateral diffusion coupling, a physiological realization of the concept of diffusive coupling, can play an important role in entraining periodicity in a nonsynaptic neural network.

FIGURE 1

Schematic diagram of three compartment lateral-diffusion-coupled network model. One compartment is assigned for the cell, one for the interstitial space and one for the bath. Dispersion (diffusion to the bath) and lateral diffusion (diffusion between the interstitial spaces of neighboring cells) were included in the model. For the cell, the 16-compartment zero-Ca²⁺ CA1 pyramidal cells were used and they were arranged in an array. For [K⁺]_o regulation mechanisms, K⁺ pump and glial buffer uptake were used. With the cell radius of 8.9 μm and the volume ratio of 0.15, the outer diameter of each sphere was estimated as 18.64 μm. All cells with respect to a (virtual) extracellular recording site (solid circle) were used for the calculation of field potential. ‘r’ indicates a distance between the recording location and the center of a cell-body.

FIGURE 2

In vivo SE-like activity and distribution of interevent intervals. (a) Thirty seconds long in vivo SE-like activity obtained in the rat hippocampus exposed to a medium with EGTA, zero Ca²⁺, and high K⁺. The onset times of consecutive two events provide time intervals ΔT shown in enlargements. (b) The distribution of inter event intervals calculated from ∼140 s long recording associated with SE-like activity shown in (a). A local maximum around 0.25 s is consistent with a frequency of ∼4 Hz. (c) Statistical sensitivity analysis of the distribution of interevent intervals obtained from six separate in vivo data sets. Each data set was recorded for 1– 2 min with the data sampling rate of 20 KHz after 60, 65, 70, 75, 80, 85 min use of EGTA.

FIGURE 3

Contribution of the diffusive coupling to extracellular field potential activity. Simulation results obtained from coupled and uncoupled networks are plotted in (a–c) and (d–f), respectively. With potassium lateral diffusion coupling, (a) simulated field potential activity shows a periodic pattern; (b) the interevent interval distribution shows a clear local maximum around 0.25 s and (c) a similar local maximum is shown in the average interevent interval distribution for 10 realizations. Without diffusive coupling, (d) no periodicity can be detected from simulated field potential activity; (e) no clear peak can be observed in the interevent interval distribution (for one realization) and (f) the same flatness can be shown in the average interevent interval distribution for 10 different realizations. For the simulations, the parameter values used were: τ_ss = 5 ms and N = 16.

FIGURE 4

Effect of potassium diffusive coupling on the synchronization of intracellular neuronal activity. With potassium lateral coupling, (a) phases of neuronal firings (activities of five neurons out of 16 are shown here) are locked and (b) the mean frequencies of the cells fall within a very narrow range (3.97∼4.04 Hz) given the parameter values used for this simulation (τ_ss = 5 ms; other parameters can be found in Table 4.) (c) The preferred phases are shown in the cyclic relative phase distribution. Without lateral diffusion coupling, (d) phases of neuronal firings keep slipping, and (e) the histogram of mean frequency values shows a pronounced peak around 4 Hz. (f) The relative phase distribution shows no local maximum around preferred phase value. For this simulation, 5 ms lateral time constant (τ_ss) and 16 cells (N) were used. The different types of lines indicate neuronal activity from different cells.

FIGURE 5

Relation between synchrony index and coupling strength and scaling behavior between the number of neurons in the network and critical coupling strength. (a) The ensemble average synchrony index 〈γ〉 as a function of coupling strength (ɛ) for N = 12 is shown. The critical coupling strength ɛ_c is determined at the value where 〈γ〉 = 0.9. Solid gray line along the curve indicates interpolated values. (b) The algebraic scaling between ln ɛ_c and ln N; ln ɛ_c = α × ln N is plotted. The scaling exponent “a” was 0.7 ± 0.08.

FIGURE 6

Diffusive coupling and periodicity in extracellular activity. (a) Schematic diagram illustrating how each diffusion path was deleted. (b) The mean synchrony index is plotted as a function of the number of active connections through potassium diffusion. The horizontal axis indicates the number of cells around which four diffusion directions toward their nearest neighbor are blocked. With an intact diffusive coupling ((i) 0-deletion), the local maximum around preferred phases are clearly shown in the distribution, whereas with completely blocked diffusion paths ((iv) 16-deletion), only a flatness is shown, i.e., no phase synchronization takes place. In between situation ((ii) 2-deletion and (iii) 8-deletion), a gradual decrease of the maximum peak of the distribution is illustrated as the number of diffusion path deletions increases.