A flexible nonlinear feedback system that captures diverse patterns of adaptation and rebound

Abstract

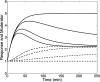
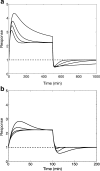
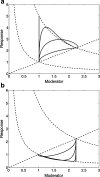
An important approach to modeling tolerance and adaptation employs feedback mechanisms in which the response to the drug generates a counter-regulating action which affects the response. In this paper we analyze a family of nonlinear feedback models which has recently proved effective in modeling tolerance phenomena such as have been observed with SSRI's. We use dynamical systems methods to exhibit typical properties of the response-time course of these nonlinear models, such as overshoot and rebound, establish quantitive bounds and explore how these properties depend on the system and drug parameters. Our analysis is anchored in three specific in vivo data sets which involve different levels of pharmacokinetic complexity. Initial estimates for system (k(in), k(out), k(tol)) and drug (EC(50)/IC(50), E(max)/I(max), n) parameters are obtained on the basis of specific properties of the response-time course, identified in the context of exploratory (graphical) data analysis. Our analysis and the application of its results to the three concrete examples demonstrates the flexibility and potential of this family of feedback models.

Fig. 1

Sketch of the basic feedback model and a typical response versus time course. The response R is governed by the zero-order turnover rate k _in and the first-order fractional turnover rate k _out, and then indirectly also controlled by a separate moderator M. The turnover of the moderator is governed by a single first-order rate constant k _tol. The build-up of the moderator is k _tol·R and loss is k _tol·M. The moderator acts via inhibition of k _in on the production of response (as in the scheme above) or via stimulation of k _out (negative feedback). The solid lines denote flows and the dashed lines denote control action. In the response versus time course we note substantial overshoot and rebound

Fig. 2

Response versus time courses of the three examples that anchor the analysis. Example I is derived from a compound A that inhibits the production of response of which data were gathered after a regimen of multiple intravenous infusions. Example II represents a test compound X acting via inhibition of k _out after a short constant rate infusion of X followed by washout. Example III represents our extended model fitted to the Bundgaard et. al. (21) data set, where escitalopram acts via inhibition of the loss of R and the moderator compartment is split into two transduction compartments

Fig. 3

Simulations of response and moderator versus time for onset of a constant long-lasting infusion (t ₁ = ∞) for k _tol = 0, 0.001, 0.005, 0.01. The other parameter values are k _in = 0.23, k _out = 0.23 (R ₀ = 1), and I _max = 0.8, C _ss » IC ₅₀. Solid lines represent the response-time courses and the dashed lines the moderator-time courses

Fig. 4

Simulations of response and moderator versus time for onset of a constant long-lasting infusion (t ₁ = ∞) for k _tol = 0.1, 0.2, 0.5, 2.0 (right). The other parameter values are k _in = 0.23, k _out = 0.23 (R ₀ = 1), and I _max = 0.8, C _ss » IC ₅₀. Solid lines represent the response-time courses and the dashed lines the moderator-time courses

Fig. 5

Simulations of response and moderator versus time during constant infusion, and subsequent washout for k _tol = 0.001, 0.005, 0.01 (a) and for k _tol = 0.03, 0.1, 0.3, 1.0 (b). The other parameter values are k _in = 0.23, k _out = 0.23 (R ₀ = 1), and I _max = 0.8, C _ss » IC ₅₀

Fig. 6

Response versus time data after a multiple intravenous infusion regimen of compound A, followed by washout. Note the substantial rebound effect shortly after the infusion has been terminated at about 200 min. The infusion pump stopped for a brief period at about 90 min until the next syringe had been loaded. Then there is a rapid return of response towards the baseline and past the baseline. The six gray bars represent six different infusion rates. Response denotes concentration of fatty acids in plasma

Fig. 7

Response versus time courses of Example II which represents test compound X acting via inhibition of k _out after a 10 min constant rate intravenous infusion of X followed by washout. Note the drift of the baseline over the 260 min observation period. Response denotes EEG effects in experimental animals

Fig. 8

Simulation of response versus time course based on the final parameter estimates in Table 2 (model A) where the exposure profile was given as a square-wave (gray horizontal bar) and no baseline drift was assumed to occur. R ₀, R _max and R _ss denote the baseline value, peak-response in overshoot and steady-state response, respectively

Fig. 9

Response versus time (left) and response versus concentration (right) courses of Example III which represent escitalopram acting via inhibition of k _out after a 60 min constant rate intravenous infusion followed by washout. Symbols represent experimental data and solid lines model fits. The three 60 min constant rate intravenous infusions were 2.5 (filled circles), 5 (filled squares) and 10 (open squares) mg/kg. The small arrows on the right hand plot show the time order of the data. Note how the middle and upper concentration-response curves cut through the lower and middle concentration-response curves, respectively

Fig. 10

Sketch of the extended feedback model involving two moderators M ₁ and M ₂ in sequence. The solid lines denote flows and the dashed lines denote control action

Fig. 11

Schematic illustration of deriving the initial parameter estimates based on the response-time course of Example II obtained after a 15 min constant rate intravenous infusion of test compound X followed by washout. The slope is mathematically defined by Eq. 42, and Δ = R _ss(t) − R ₀(t) = R _ss(0) − R ₀(0)

Fig. 12

Orbits in the (R, M)-plane for onset of infusion (a) and for washout (b). The constants are κ = k _tol/k _out = 0, 0.01, 0.1, 1 and k _in = 0.23, k _out = 0.23 (R ₀ = 1), and I _max = 0.8, C _ss » IC ₅₀. The dashed lines are the null clines through (R ₀,M ₀) and through (R _ss,M _ss)

Fig. 13

Response versus time plot (a) and the corresponding orbit in the (R,M) -plane for onset (b) of infusion and washout after 10 min. The constants are k _tol = 1, k _in = 10, k _out = 10 and I _max = 0.5 and C _ss » IC ₅₀. The dashed lines are the null clines through, respectively, (R ₀,M ₀) and (R _ss,M _ss)