Signal processing by the HOG MAP kinase pathway
- PMID: 18480263
- PMCID: PMC2386076
- DOI: 10.1073/pnas.0710770105
Signal processing by the HOG MAP kinase pathway
Abstract
Signaling pathways relay information about changes in the external environment so that cells can respond appropriately. How much information a pathway can carry depends on its bandwidth. We designed a microfluidic device to reliably change the environment of single cells over a range of frequencies. Using this device, we measured the bandwidth of the Saccharomyces cerevisiae signaling pathway that responds to high osmolarity. This prototypical pathway, the HOG pathway, is shown to act as a low-pass filter, integrating the signal when it changes rapidly and following it faithfully when it changes more slowly. We study the dependence of the pathway's bandwidth on its architecture. We measure previously unknown bounds on all of the in vivo reaction rates acting in this pathway. We find that the two-component Ssk1 branch of this pathway is capable of fast signal integration, whereas the kinase Ste11 branch is not. Our experimental techniques can be applied to other signaling pathways, allowing the measurement of their in vivo kinetics and the quantification of their information capacity.
Conflict of interest statement
The authors declare no conflict of interest.
Figures


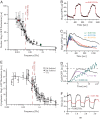

 ) or SHO1 (▴) blocks input to Hog1 from the SHO1 branch. Strains with this branch blocked show no change in bandwidth compared with the wild-type strain. Time scales are in good agreement for wild type (ωb = 4.6 × 10−3 ± 1.10 × 10−3 Hz), sho1Δ mutants (ωb = 4.6 × 10−3 ± 0.9 × 10−3 Hz), and ste11Δ mutants (ωb = 4.6 × 10−3 ± 1 × 10−3 Hz), indicating that the SSK1 branch dominates the activation dynamics of the HOG pathway. (B) Deletion of SSK1 (●) blocks input to Hog1 from the SLN1 branch. The ssk1Δ strains (ωb = 2.6 × 10−3 ± 0.4 × 10−3 Hz) show close to 2-fold decrease in bandwidth compared with the wild-type strain (■, ωb = 4.6 × 10−3 ± 1.1 × 10−3 Hz). Each point represents the amplitude of Hog1-GFP and Htb2-mCherry colocalization over, typically, 10 cells. The error bars represent one standard deviation from the mean. (C) The time course of nuclear Hog1-GFP levels for the input oscillating 0.2 Hz (larger than the pathway bandwidth) is shown for cells of ste11Δ (in green) and ssk1Δ (in red) strain backgrounds. At such high frequencies, the cells possessing only the Ssk1 branch (ste11Δ) integrate the input just as the wild type (see Fig. 3C), whereas the cells possessing just the Sho1 branch (ssk1Δ) do not respond at all. Thus it is the Ssk1 branch of the pathway that allows the cells to integrate fluctuating inputs from the environment. (D) Time course of nuclear Hog1::GFP intensity as a function of time shown for different temporally changing inputs. In both Upper and Lower graphs, the input amplitude (shown in red) oscillates between 0 and 1 M sorbitol starting at time t = 0 s. In Upper, the input stays at 1 M for ton = 100 s and at 0 M for toff = 50 s. In Lower, ton = 100 s, whereas toff = 400 s. The nuclear Hog1::GFP intensity oscillates according to the input. The amplitude of the oscillation for toff = 400 is larger than for toff = 50 s. (E) The amplitude of the oscillations in Hog1 nuclear intensity is plotted as a function of toff for a fixed ton = 100 s. With increasing toff, the amplitude of Hog1::GFP oscillations in steady-state increase, reaching a maximum at and above toff = 800 s. (F) The log of the difference in the amplitude of the oscillation at a given toff (shown in D) from that at toff = 800 s is plotted as a function of toff. This plot gives an accurate measure of the rate constant for the turn off of the osmolar pathway when the osmolar input is turned off, and from the slope of this plot, we find it to be 0.0041 ± 0.0005 Hz, which corresponds to within error bars to the bandwidth of the Hog pathway shown in Fig. 3. This shows that the rate-limiting step is the turn off of the Hog pathway.
) or SHO1 (▴) blocks input to Hog1 from the SHO1 branch. Strains with this branch blocked show no change in bandwidth compared with the wild-type strain. Time scales are in good agreement for wild type (ωb = 4.6 × 10−3 ± 1.10 × 10−3 Hz), sho1Δ mutants (ωb = 4.6 × 10−3 ± 0.9 × 10−3 Hz), and ste11Δ mutants (ωb = 4.6 × 10−3 ± 1 × 10−3 Hz), indicating that the SSK1 branch dominates the activation dynamics of the HOG pathway. (B) Deletion of SSK1 (●) blocks input to Hog1 from the SLN1 branch. The ssk1Δ strains (ωb = 2.6 × 10−3 ± 0.4 × 10−3 Hz) show close to 2-fold decrease in bandwidth compared with the wild-type strain (■, ωb = 4.6 × 10−3 ± 1.1 × 10−3 Hz). Each point represents the amplitude of Hog1-GFP and Htb2-mCherry colocalization over, typically, 10 cells. The error bars represent one standard deviation from the mean. (C) The time course of nuclear Hog1-GFP levels for the input oscillating 0.2 Hz (larger than the pathway bandwidth) is shown for cells of ste11Δ (in green) and ssk1Δ (in red) strain backgrounds. At such high frequencies, the cells possessing only the Ssk1 branch (ste11Δ) integrate the input just as the wild type (see Fig. 3C), whereas the cells possessing just the Sho1 branch (ssk1Δ) do not respond at all. Thus it is the Ssk1 branch of the pathway that allows the cells to integrate fluctuating inputs from the environment. (D) Time course of nuclear Hog1::GFP intensity as a function of time shown for different temporally changing inputs. In both Upper and Lower graphs, the input amplitude (shown in red) oscillates between 0 and 1 M sorbitol starting at time t = 0 s. In Upper, the input stays at 1 M for ton = 100 s and at 0 M for toff = 50 s. In Lower, ton = 100 s, whereas toff = 400 s. The nuclear Hog1::GFP intensity oscillates according to the input. The amplitude of the oscillation for toff = 400 is larger than for toff = 50 s. (E) The amplitude of the oscillations in Hog1 nuclear intensity is plotted as a function of toff for a fixed ton = 100 s. With increasing toff, the amplitude of Hog1::GFP oscillations in steady-state increase, reaching a maximum at and above toff = 800 s. (F) The log of the difference in the amplitude of the oscillation at a given toff (shown in D) from that at toff = 800 s is plotted as a function of toff. This plot gives an accurate measure of the rate constant for the turn off of the osmolar pathway when the osmolar input is turned off, and from the slope of this plot, we find it to be 0.0041 ± 0.0005 Hz, which corresponds to within error bars to the bandwidth of the Hog pathway shown in Fig. 3. This shows that the rate-limiting step is the turn off of the Hog pathway.References
-
- Shannon CE. A mathematical theory of communication. Bell Syst Tech J. 1948;27:379–423. 623–656.
-
- Alberts B, et al. Molecular Biology of the Cell. 4th Ed. New York: Garland; 2002.
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases

