Bayesian LASSO for quantitative trait loci mapping

Abstract

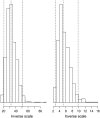
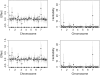
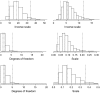
The mapping of quantitative trait loci (QTL) is to identify molecular markers or genomic loci that influence the variation of complex traits. The problem is complicated by the facts that QTL data usually contain a large number of markers across the entire genome and most of them have little or no effect on the phenotype. In this article, we propose several Bayesian hierarchical models for mapping multiple QTL that simultaneously fit and estimate all possible genetic effects associated with all markers. The proposed models use prior distributions for the genetic effects that are scale mixtures of normal distributions with mean zero and variances distributed to give each effect a high probability of being near zero. We consider two types of priors for the variances, exponential and scaled inverse-chi(2) distributions, which result in a Bayesian version of the popular least absolute shrinkage and selection operator (LASSO) model and the well-known Student's t model, respectively. Unlike most applications where fixed values are preset for hyperparameters in the priors, we treat all hyperparameters as unknowns and estimate them along with other parameters. Markov chain Monte Carlo (MCMC) algorithms are developed to simulate the parameters from the posteriors. The methods are illustrated using well-known barley data.

Figure 1.—

Posterior medians (points) and 95% intervals (shaded lines) for genetic effects and the proportion of the phenotypic variance explained by each effect (i.e., heritability). (Top) Plots drawn from model I; (bottom) plots for model II. Inner tick marks on the x-axis represent the marker positions.

Figure 2.—

Histogram of the posterior samples for the inverse scale of the exponential prior on the variances. The dotted lines represent the posterior 5, 50, and 95% quantiles. The left and right plots show inferences for models I and II, respectively.

Figure 3.—

Posterior medians (points) and 95% intervals (shaded lines) for genetic effects and the proportion of the phenotypic variance explained by each effect (i.e., heritability). (Top) Plots drawn from model III; (bottom) plots for model IV. Inner tick marks on the x-axis represent the marker positions.

Figure 4.—

Histogram of the posterior samples for the degrees of freedom and scale of the Inv- prior on variances. The dotted lines represent the posterior 5, 50, and 95% quantiles. The top and bottom plots show inferences for models III and IV, respectively.

Figure 5.—

The top plot shows posterior medians (points) and 95% intervals (shaded lines) for the approximate Bayesian LOD score from model I, and the bottom plot shows the LOD score curve from traditional interval mapping. The dotted lines represent the standard threshold value of 3.2. Inner tick marks on the x-axis represent the marker positions.

Figure 6.—

Posterior medians (points) and 95% intervals (shaded lines) for genetic effects from all four models using markers on chromosomes 1, 3, and 7. Inner tick marks on the x-axis represent the marker positions.

Figure 7.—

Histogram of the posterior samples for the hyperparameters of priors on variances. The dotted lines represent the posterior 5, 50, and 95% quantiles. The top plots show inferences for models I and II, respectively, the middle plots show inferences from model III, and the bottom plots show inferences from model IV.