Inferring causal phenotype networks from segregating populations
- PMID: 18505877
- PMCID: PMC2429862
- DOI: 10.1534/genetics.107.085167
Inferring causal phenotype networks from segregating populations
Abstract
A major goal in the study of complex traits is to decipher the causal interrelationships among correlated phenotypes. Current methods mostly yield undirected networks that connect phenotypes without causal orientation. Some of these connections may be spurious due to partial correlation that is not causal. We show how to build causal direction into an undirected network of phenotypes by including causal QTL for each phenotype. We evaluate causal direction for each edge connecting two phenotypes, using a LOD score. This new approach can be applied to many different population structures, including inbred and outbred crosses as well as natural populations, and can accommodate feedback loops. We assess its performance in simulation studies and show that our method recovers network edges and infers causal direction correctly at a high rate. Finally, we illustrate our method with an example involving gene expression and metabolite traits from experimental crosses.
Figures







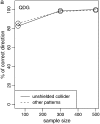




References
-
- Brem, R. B., G. Yvert, R. Clinton and L. Kruglyak, 2002. Genetic dissection of transcriptional regulation in budding yeast. Science 296 752–755. - PubMed
-
- Chesler, E. J., L. Lu, S. Shou, Y. Qu, J. Gu et al., 2005. Complex trait analysis of gene expression uncovers polygenic and pleiotropic networks that modulate nervous system function. Nat. Genet. 37 233–242. - PubMed
-
- de la Fuente, A., N. Bing, I. Hoeschele and P. Mendes, 2004. Discovery of meaningful associations in genomic data using partial correlation coefficients. Bioinformatics 20 3565–3574. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

