The hydrophobic insertion mechanism of membrane curvature generation by proteins
- PMID: 18515373
- PMCID: PMC2517036
- DOI: 10.1529/biophysj.108.133173
The hydrophobic insertion mechanism of membrane curvature generation by proteins
Abstract
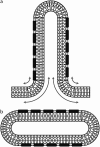
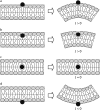
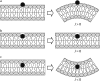
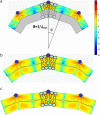
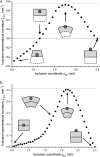
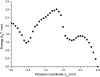
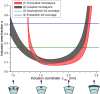
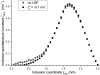
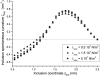
A wide spectrum of intracellular processes is dependent on the ability of cells to dynamically regulate membrane shape. Membrane bending by proteins is necessary for the generation of intracellular transport carriers and for the maintenance of otherwise intrinsically unstable regions of high membrane curvature in cell organelles. Understanding the mechanisms by which proteins curve membranes is therefore of primary importance. Here we suggest, for the first time to our knowledge, a quantitative mechanism of lipid membrane bending by hydrophobic or amphipathic rodlike inclusions which simulate amphipathic alpha-helices-structures shown to sculpt membranes. Considering the lipid monolayer matrix as an anisotropic elastic material, we compute the intramembrane stresses and strains generated by the embedded inclusions, determine the resulting membrane shapes, and the accumulated elastic energy. We characterize the ability of an inclusion to bend membranes by an effective spontaneous curvature, and show that shallow rodlike inclusions are more effective in membrane shaping than are lipids having a high propensity for curvature. Our computations provide experimentally testable predictions on the protein amounts needed to generate intracellular membrane shapes for various insertion depths and membrane thicknesses. We also predict that the ability of N-BAR domains to produce membrane tubules in vivo can be ascribed solely to insertion of their amphipathic helices.
Figures


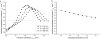

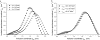
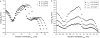
References
-
- Helfrich, W. 1973. Elastic properties of lipid bilayers: theory and possible experiments. Z. Naturforsch. 28c:693–703. - PubMed
-
- Kirchhausen, T. 2000. Three ways to make a vesicle. Nat. Rev. Mol. Cell Biol. 1:187–198. - PubMed
-
- McMahon, H. T., and J. L. Gallop. 2005. Membrane curvature and mechanisms of dynamic cell membrane remodeling. Nature. 438:590–596. - PubMed
-
- Zimmerberg, J., and M. M. Kozlov. 2006. How proteins produce cellular membrane curvature. Nat. Rev. Mol. Cell Biol. 7:9–19. - PubMed
-
- Antonny, B. 2006. Membrane deformation by protein coats. Curr. Opin. Cell Biol. 18:386–394. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources

