An analytic and systematic framework for estimating metabolic flux ratios from 13C tracer experiments

Abstract

Background: Metabolic fluxes provide invaluable insight on the integrated response of a cell to environmental stimuli or genetic modifications. Current computational methods for estimating the metabolic fluxes from 13C isotopomer measurement data rely either on manual derivation of analytic equations constraining the fluxes or on the numerical solution of a highly nonlinear system of isotopomer balance equations. In the first approach, analytic equations have to be tediously derived for each organism, substrate or labelling pattern, while in the second approach, the global nature of an optimum solution is difficult to prove and comprehensive measurements of external fluxes to augment the 13C isotopomer data are typically needed.

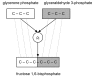
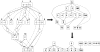
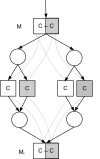
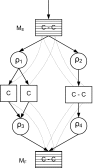
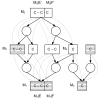
Results: We present a novel analytic framework for estimating metabolic flux ratios in the cell from 13C isotopomer measurement data. In the presented framework, equation systems constraining the fluxes are derived automatically from the model of the metabolism of an organism. The framework is designed to be applicable with all metabolic network topologies, 13C isotopomer measurement techniques, substrates and substrate labelling patterns. By analyzing nuclear magnetic resonance (NMR) and mass spectrometry (MS) measurement data obtained from the experiments on glucose with the model micro-organisms Bacillus subtilis and Saccharomyces cerevisiae we show that our framework is able to automatically produce the flux ratios discovered so far by the domain experts with tedious manual analysis. Furthermore, we show by in silico calculability analysis that our framework can rapidly produce flux ratio equations--as well as predict when the flux ratios are unobtainable by linear means--also for substrates not related to glucose.

Conclusion: The core of 13C metabolic flux analysis framework introduced in this article constitutes of flow and independence analysis of metabolic fragments and techniques for manipulating isotopomer measurements with vector space techniques. These methods facilitate efficient, analytic computation of the ratios between the fluxes of pathways that converge to a common junction metabolite. The framework can been seen as a generalization and formalization of existing tradition for computing metabolic flux ratios where equations constraining flux ratios are manually derived, usually without explicitly showing the formal proofs of the validity of the equations.

Figure 1

An example of a metabolic reaction. In the reaction ρ_j, a fructose 1,6-bisphosphate (C₆H₁₄O₁₂P₂) molecule is produced from glycerone phosphate (C₃H₇O₆P) and glyceraldehyde 3-phosphate (C₃H₇O₆P) molecules. Carbon maps are shown with dashed lines. Glyceraldehyde 3-phosphate is equivalent to the gray fragment of fructose 1,6-bisphosphate while glycerone phosphate is equivalent to the white fragment.

Figure 2

An example of subpools of a metabolite pool. Phosphoenolpyruvate (PEP) is produced by two different reactions (ρ_i and ρ_j), either from Oxaloacetate (OAA) or from glyceraldehyde 3-phosphate (GA3P). Thus, PEP has two in flow subpools, PEP from OAA and PEP from GA3P (grey boxes) that are mixed in the common PEP pool (at the bottom).

Figure 3

An example of fragment equivalence classes in a branched pathway. An example of equivalence classes of fragments in the metabolic network that contains dominated junction fragments M|E and M|F. Grey and white fragments constitute two equivalence classes. Dashed lines depict carbon mappings.

Figure 4

An example of a fragment flow graph and a dominator tree. A metabolic network (left), the corresponding fragment flow graph (up right) and the subtrees of the dominator tree (down right).

Figure 5

An example of statistical independence of fragments. White and grey one-carbon-fragments of M_i are statistically independent: both fragments are dominated by one-carbon-fragments of M, and the fragments are disjoint in every pathway that produce M_i from M.

Figure 6

An example of using fragment independence to obtain new isotopomer constraints under uniform substrate labelling. Constraints to the isotopomer distributions of striped metabolites are assumed to be known, either by direct measurement of measurement propagation. In pathway q = (ρ₂, ρ₄), the isotopomer distribution of M_F molecules will be the same as in M_E. In pathway p = (ρ₁, ρ₃), the isotopomer distribution of M_F can be derived by applying fragment independence: the isotopomer distributions of single carbon metabolites produced by ρ₁ are known a priori to be equal to the labelling degree of uniformly labelled substrate. As the two carbons of M_F3 are produced from two different metabolites, these carbons are statistically independent to each other in the subpool and the isotopomer distribution D($M_{F_p}$) of M_F molecules produced by p can be computed by applying Equation 7.

Figure 7

An example of using fragment independence to obtain new isotopomer constraints for a reactant. The mass isotopomer distributions of striped metabolites are assumed to be measured. Fragments M₁|E and M₂ belong to the same fragment equivalence class. Thus, D_m(M₁|E) can be derived from D_m(M₂) by the measurement propagation inside equivalence classes. Furthermore, fragments M₅|E' and M₅|F' dominate fragments M₁|E and M₁|F, and the bond between M₁|E and M₁|F is broken in all pathways producing M₁ from M₅. Thus, M₁|E and M₁|F are statistically independent, and D_m(M₁|F) can be deduced from D_m(M₁) and D_m(M₁|E) by utilizing Equation 7. Computed D_m(M₁|F) can then be propagated to M₄, as M₁ and M₄ belong to the same fragment equivalence class. Finally, D_m(M₄) helps to solve the ratios of fluxes entering to M₃.

Figure 8

An example of the computation of the common subspace of isotopomer constraints in different subpools. The mass isotopomer distribution of junction metabolite M₁ is assumed to be measured. For the in flow subpools M₁₁ and M₁₂ we obtain isotopomer constraints from the above reactant metabolites by measurement propagation. These propagated constraints must be projected to mass isotopomer to the subspace defined by the mass isotopomer distribution of M₁ before generalized isotopomer balances are constructed.