DYNAMIC BEHAVIOR OF A PACED CARDIAC FIBER

Abstract

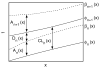
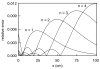
Consider a typical experimental protocol in which one end of a one-dimensional fiber of cardiac tissue is periodically stimulated, or paced, resulting in a train of propagating action potentials. There is evidence that a sudden change in the pacing period can initiate abnormal cardiac rhythms. In this paper, we analyze how the fiber responds to such a change in a regime without arrhythmias. In particular, given a fiber length L and a tolerance eta, we estimate the number of beats N = N(eta, L) required for the fiber to achieve approximate steady-state in the sense that spatial variation in the diastolic interval (DI) is bounded by eta. We track spatial DI variation using an infinite sequence of linear integral equations which we derive from a standard kinematic model of wave propagation. The integral equations can be solved in terms of generalized Laguerre polynomials. We then estimate N by applying an asymptotic estimate for generalized Laguerre polynomials. We find that, for fiber lengths characteristic of cardiac tissue, it is often the case that N effectively exhibits no dependence on L. More exactly, (i) there is a critical fiber length L* such that, if L < L*, the convergence to steady-state is slowest at the pacing site, and (ii) often, L* is substantially larger than the diameter of the whole heart.

Fig. 1

Voltage trace of several action potentials in a paced cardiac cell.

Fig. 2

Spatial variation in DI after changing the pacing period from B_old to B_new < B_old. (a) the curves D_n(x) for n = 1, . . . , 4; (b) the curves D_n(x) for n = 7, 8.

Fig. 3

Schematic diagram of wave fronts (solid curves) and wave backs (dashed curves).

Fig. 4

Relative error in using y_n(x) to approximate $D_n(x)-D_{\text{new}}^{\ast }$ * for n = 1, . . . , 4.

Fig. 5

Comparison of the generalized Laguerre polynomial $L_n^{(\beta )}(x)$ with the approximation given by Theorem 3.2 for n = 10 and β = 1. As indicated in the figure, the first two roots of the approximation (36) occur when the argument of the cosine function is −π/2 or π/2.