Association mapping by generalized linear regression with density-based haplotype clustering

Abstract

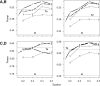
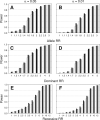
Haplotypes of closely linked single-nucleotide polymorphisms (SNPs) potentially offer greater power than individual SNPs to detect association between genetic variants and disease. We present a novel approach for association mapping in which density-based clustering of haplotypes reduces the dimensionality of the general linear model (GLM)-based score test of association implemented in the HaploStats software (Schaid et al. [2002] Am. J. Hum. Genet. 70:425-434). A flexible haplotype similarity score, a generalization of previously used measures, forms the basis, for grouping haplotypes of probable recent common ancestry. All haplotypes within a cluster are assigned the same regression coefficient within the GLM, and evidence for association is assessed with a score statistic. The approach is applicable to both binary and continuous trait data, and does not require prior phase information. Results of simulation studies demonstrated that clustering enhanced the power of the score test to detect association, under a variety of conditions, while preserving valid Type-I error. Improvement in performance was most dramatic in the presence of extreme haplotype diversity, while a slight improvement was observed even at low diversity. Our method also offers, for binary traits, a slight advantage in power over a similar approach based on an evolutionary model (Tzeng et al. [2006] Am. J. Hum. Genet. 78:231-242).

Fig. 1

Optimizing power to detect association with a multiplicative binary-trait locus. Power from the score test was estimated over 1,000 independently generated data sets of 200 cases and 200 controls. In every panel, thin-dotted lines marked as H and Tz indicate power from the HST and the TzST, respectively. Power for the CST is plotted over ranges of ε by different lines and symbols representing values of p_min: p_min = 1/N (N = number of distinct haplotypes), thick solid line, symbol = 1; p_min = 1/2N, thick-dashed line, symbol = 2; p_min = 1/3N, thin solid line, symbol = 3; p_min determined by the Shannon information criterion, thin-dashed line, symbol = S. (A, B), Power to detect association under the “low-power” model at nominal Type-I error of 0.05 (A) and 0.01 (B). (C, D), Power to detect association under the “high-power” model at nominal Type-I error of 0.05 (C) and 0.01 (D). The range of the y-axis was determined by the range of performance, and therefore is different in each panel.

Fig. 2

Mean degrees of freedom (d.f.) of the score test from 1,000 data sets of 200 cases and 200 controls, under the “low-power” (A) and “high-power” (B) scenarios. Lines and symbols for p_min = 1/N, 1/2N, 1/3N and determined by the Shannon information criterion are as in Figure 1; p_min = 1 is represented by a thick-dotted line and the symbol 0. Thin-dotted lines indicate mean d.f. of the HST (H) and the TzST (Tz).

Fig. 3

Power to detect association at the 0.05 significance level with a multiplicative binary-trait locus, stratified by haplotype diversity. For each panel, 1,000 data sets of 200 cases and 200 controls were analyzed. Panels are indicated in terms of haplotype diversity (low, medium, or high) and simulation model (low or high power). In all panels, power of the HST and the TzST is depicted as in Figure 1, and power of the CST is shown as follows: p_min = 1/N, solid lines, symbol = 1; p_min = 1/2N, long-dashed lines, symbol = 2; p_min = 1/3N, short-dashed lines, symbol = 3.

Fig. 4

Comparison of power to detect association with binary-trait data using the HST, the CST, and the TzST. Each triplet of bars represents power estimates from 1,000 data sets of 200 cases and 200 controls. Power is shown at the 0.05 (left column) and 0.01 (right column) significance levels, as a function of signal strength for a multiplicative (A, B), a dominant (C, D), and a recessive (E, F) trait locus. The frequency of the disease allele D is 0.2 throughout. Allele RR, relative risk (RR) associated with each D allele at the trait locus; Dominant RR, RR associated with trait-locus genotype Dd or DD; Recessive RR, RR associated with genotype DD. White bars, HST; black bars, CST; gray bars, TzST.