Tumor trailing strategy for intensity-modulated radiation therapy of moving targets

Abstract

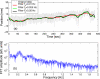
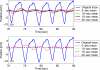
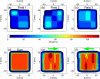
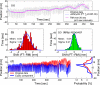
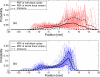
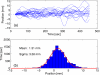
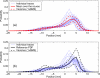
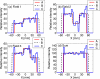
Internal organ motion during the course of radiation therapy of cancer affects the distribution of the delivered dose and, generally, reduces its conformality to the targeted volume. Previously proposed approaches aimed at mitigating the effect of internal motion in intensity-modulated radiation therapy (IMRT) included expansion of the target margins, motion-correlated delivery (e.g., respiratory gating, tumor tracking), and adaptive treatment plan optimization employing a probabilistic description of motion. We describe and test the tumor trailing strategy, which utilizes the synergy of motion-adaptive treatment planning and delivery methods. We regard the (rigid) target motion as a superposition of a relatively fast cyclic component (e.g., respiratory) and slow aperiodic trends (e.g., the drift of exhalation baseline). In the trailing approach, these two components of motion are decoupled and dealt with separately. Real-time motion monitoring is employed to identify the "slow" shifts, which are then corrected by applying setup adjustments. The delivery does not track the target position exactly, but trails the systematic trend due to the delay between the time a shift occurs, is reliably detected, and, subsequently, corrected. The "fast" cyclic motion is accounted for with a robust motion-adaptive treatment planning, which allows for variability in motion parameters (e.g., mean and extrema of the tidal volume, variable period of respiration, and expiratory duration). Motion-surrogate data from gated IMRT treatments were used to provide probability distribution data for motion-adaptive planning and to test algorithms that identified systematic trends in the character of motion. Sample IMRT fields were delivered on a clinical linear accelerator to a programmable moving phantom. Dose measurements were performed with a commercial two-dimensional ion-chamber array. The results indicate that by reducing intrafractional motion variability, the trailing strategy enhances relevance and applicability of motion-adaptive planning methods, and improves conformality of the delivered dose to the target in the presence of irregular motion. Trailing strategy can be applied to respiratory-gated treatments, in which the correction for the slow motion can increase the duty cycle, while robust probabilistic planning can improve management of the residual motion within the gate window. Similarly, trailing may improve the dose conformality in treatment of patients who exhibit detectable target motion of low amplitude, which is considered insufficient to provide a clinical indication for the use of respiratory-gated treatment (e.g., peak-to-peak motion of less than 10 mm). The mechanical limitations of implementing tumor trailing are less rigorous than those of real-time tracking, and the same technology could be used for both.

Figure 1

(a) The drift in the position of the external marker (black line) reflects the change in position of three radio-opaque clips implanted in patient’s liver, as detected in three 20-s long sessions of fluoroscopic imaging. Location of the clips is shown in (b) coronal and (c) sagittal fluoroscopic view of the patient.

Figure 2

(a) A sample marker trace overlaid with the curves designating the ultracyclic component of the marker motion, extracted using the FT method [Eqs. 1, 2, 3] with different low-pass cutoff frequencies f_p. The Fourier transform spectrum of the original data is shown in (b).

Figure 3

The phase-pulling effect on the running mean value of the marker position is illustrated for different settings of the time window used for weighted averaging. The values are shown for the window widths of T=5, 10, 15, and 20 s for (a) no weighting (true mean) and (b) a Gaussian weighting function (with ⟨t⟩=t−T∕2, σ=T∕4).

Figure 4

Test IMRT plan (calculation): two-dimensional dose distributions from three fields shown in (a)–(c) combine to a uniform distribution (d), when delivered consecutively to the target from the same direction. In the presence of the target position drift, the distributions will not match as planned: plots (e), (f) show possible patterns of inhomogeneities for the scenarios in which the target drifted (in the beam’s eye view) in the direction indicated by arrows.

Figure 5

(a) A sample marker trace is overlaid with curves showing the ultracyclic component of motion, extracted with FT and RM methods. The RM curve is delayed with respect to the FT curve by 10 s: half of the averaging time window. The distribution of differences in the values given by the two methods is shown (b) in real time, and (c) with the 10-s delay removed (RM curve shifted back in time). The parameter values are shown for the fit to a normal distribution. Plot (d) shows the original trace, the cyclic component (after the drift detected with the RM method was subtracted), and their respective PDFs.

Figure 6

Similar to Fig. 5, but with the drift direction reversed. (a) The marker trace is overlaid with the ultracyclic motion components obtained with FT and RM methods. The distribution of differences in the values given by the two methods is shown (b) in real time, and (c) with the 10-s delay removed. Plot (d) shows the original trace, the cyclic component alone, and their respective PDFs.

Figure 7

For the data plotted in Fig. 5d, intrafractional variability of PDF is illustrated for: (a) the original data and (b) the cyclic component of the trace. Thin lines show the PDFs of 94 individual respiratory cycles, thick solid line is the PDF averaged over the entire data set, and dashed lines show the variance (1×RMS). The mean PDFs (solid lines) are the same as in Fig. 5d

Figure 8

(a) Ultracyclic motion components extracted from traces recorded during 25 fractions of a treatment course (for the same patient). The start position is set to 0 for all data sets. The distribution of drift positions is shown in (b), fitted to the normal distribution.

Figure 9

Interfractional variation of PDF is illustrated for the patient who received 25 fractions of respiratory-gated treatment: (a) the PDFs of individual fractions are shown as thin lines, as well as the mean PDF (solid line) and its variance (dashed line) over the course. For comparison, plot (b) shows the same data overlaid with the mean of the reference trace and its intrafractional variance [same as in Fig. 7b].

Figure 10

Intensity profiles through the isocenter, along the direction of target motion, from (a)–(c) three test fields, and (d) their sum. Profiles are shown for three types of plans described in Sec. 2: unoptimized (A) without margins, (B) with a 1-cm margin added in the direction of motion, and (C) the robust-optimized plan.

Figure 11

Results of dose measurement from delivery of the unoptimized test plan to the phantom that moved according to the trace in Fig. 5a. The doses from three fields are shown separately in (a)–(c). The combined dose (d) shows the distribution of inhomogeneities similar to that in Fig. 4f, due to the drift in the target position. Dose profiles through the isocenter are shown for (e) X and (f) Y directions. Both the phantom and MLC leaves moved in the X direction. The resolution of the dose measurement is 7.62 mm.

Figure 12

Similar to Fig. 11, for the test plan optimized using the robust method and delivered to a moving target using the trailing strategy: the drift was corrected by adjusting the phantom position.

Figure 13

DVHs from the measurement of the dose delivered in four fractions with the regular plans without and with margins, and the robust plan. The margin plan was delivered without and with the trailing correction for the target drift. The robust plan was delivered with the trailing correction.

Figure 14

The dose profiles through the isocenter, show inhomogeneities produced by the interplay of the MLC sequence with the target motion, during four fractions of delivery of the robust test plan from Fig. 12. The profiles are shown for each of the three fields, as well as for the fraction total.

Figure 15

Distribution of the bixels, 5×5 mm² beam elements of the MLC field, by the number of delivered monitor units. The scale on top of the plot shows the corresponding beam-on times for the delivery rate of 300 MU∕min.

Figure 16

Simulation of the effective PDF sampling by individual bixels, with beam-on times between 0.5 and 16 s per fraction. Motion traces from 25 fractions were sampled randomly: thin lines show possible PDF as would be sampled by individual bixels (using different seeds for random number generator). Thick dashed lines designate the PDF variance bounds, designed based on the reference trace [see Fig. 7b]. For longer beam-on times, the sampled PDF approaches the mean PDF overall fractions [Fig. 9a].

Figure 17

Probability distribution functions from traces collected during 4D-CT acquisition from 186 patients are shown as thin lines. The traces were scaled to unit amplitude (with 0 displacement corresponding to mean inhalation and 1 to mean exhalation position), after the ultracyclic component of motion was subtracted. The mean PDF is shown as the thick solid line and the variance bounds as dashed lines.