Covariance of maximum likelihood evolutionary distances between sequences aligned pairwise

Abstract

Background: The estimation of a distance between two biological sequences is a fundamental process in molecular evolution. It is usually performed by maximum likelihood (ML) on characters aligned either pairwise or jointly in a multiple sequence alignment (MSA). Estimators for the covariance of pairs from an MSA are known, but we are not aware of any solution for cases of pairs aligned independently. In large-scale analyses, it may be too costly to compute MSAs every time distances must be compared, and therefore a covariance estimator for distances estimated from pairs aligned independently is desirable. Knowledge of covariances improves any process that compares or combines distances, such as in generalized least-squares phylogenetic tree building, orthology inference, or lateral gene transfer detection.

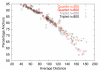
Results: In this paper, we introduce an estimator for the covariance of distances from sequences aligned pairwise. Its performance is analyzed through extensive Monte Carlo simulations, and compared to the well-known variance estimator of ML distances. Our covariance estimator can be used together with the ML variance estimator to form covariance matrices.

Conclusion: The estimator performs similarly to the ML variance estimator. In particular, it shows no sign of bias when sequence divergence is below 150 PAM units (i.e. above ~29% expected sequence identity). Above that distance, the covariances tend to be underestimated, but then ML variances are also underestimated.

Figure 1

Overview of approaches to estimate evolutionary distances and their covariances. A set of n sequences can be aligned jointly to obtain an MSA or in a pairwise optimal manner resulting in $\left(\begin{array}{c}n\\ 2\end{array}\right)$ optimal pairwise alignments (OPAs). Given a hypothesis of character homology, distance estimation per ML can essentially be done in two ways: jointly on a tree or pairwise. In the first case a tree's branch-lengths are estimated simultaneously. This requires an MSA. In the second case pairwise distances are estimated either from MSA induced pairwise alignments (IPAs) or from the OPAs. The distance estimators are afflicted with an error expressed by their variances and covariances. In all cases, the covariances can be modeled as a function of shared branch lengths, but this requires a phylogenetic tree. When distances are estimated based on an MSA, the variances and covariances can be obtained from ML theory or by bootstrapping over the MSA's columns. In the case of OPAs, these techniques cannot be directly applied (see Methods). We have previously presented a covariance estimator for the case where the two OPAs in question share a sequence (i.e. for triplets). In this paper, we introduce an estimator for the general case.

Figure 2

Possible topological relations of sequences. For two pairwise distances, one can distinguish three possible underlying topological configurations relating them. If they are estimated between four sequences, there are two possible configurations. Either they share some common evolution (a) or they are independent (b). In the third configuration, the two distances are estimated from two OPAs that share a sequence (c).

Figure 3

Comparison of the covariance estimator and the ML variance estimator with their Monte Carlo counterparts. Error-bars indicate 95% confidence intervals. a) Monte Carlo covariance estimator vs. average of the covariance estimator for sequence lengths of {200, 500, 800} AA. In the dependence case, the estimator appears unbiased in most cases. In the independence case, the estimator shows a slight upward bias, but the absolute values are close to zero. In the triplet case, a downward bias with increasing covariance is visible. b) Monte Carlo variance estimator vs. average of ML variance estimator. A downward bias with increasing variance is visible.

Figure 4

Bias and standard deviation of the covariance and ML variance estimators. Average percentage of anchors vs. bias and standard deviation of the covariance estimator for sequence length of 500 AA. Error-bars indicate the 95% confidence intervals. The bias increases with decreasing fraction of anchors. The bias is smaller than the standard deviation when percentage of anchors is greater than 65% (dependence), 80% (triplet) and 75% (ML variance).

Figure 5

Relation between distance and percentage of anchors. Horizontal axis: Average of the two distances for which the covariance has been estimated. Vertical axis: Average percentage of anchors. The Quartet labels refer to the dependence case. The fraction of anchors decreases with increasing distance.

Figure 6

Relative error of covariance matrix. Average relative error of variance matrices and variance/covariance matrices for a sequence length of 500 AA. Dependence and independence cases: Variance matrices and variance-covariance matrices have comparable error. Triplet case: Variance-covariance matrices have lower error.

Figure 7

Example of anchors. The six pairwise alignments of four example sequences (left) and the corresponding graph-representation (right). The consistent positions are in bold.