The role of feedback in the formation of morphogen territories

Abstract

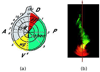
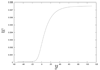
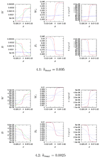
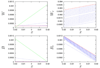
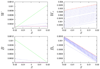
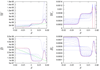
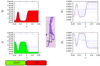
In this paper, we consider a mathematical model for the formation of spatial morphogen territories of two key morphogens: Wingless (Wg) and Decapentaplegic (DPP), involved in leg development of Drosophila. We define a gene regulatory network (GRN) that utilizes autoactivation and cros-sinhibition (modeled by Hill equations) to establish and maintain stable boundaries of gene expression. By computational analysis we find that in the presence of a general activator, neither autoactivation, nor cross-inhibition alone are sufficient to maintain stable sharp boundaries of morphogen production in the leg disc. The minimal requirements for a self-organizing system are a coupled system of two morphogens in which the autoactivation and cross-inhibition have Hill coefficients strictly greater than one. In addition, the GRN modeled here describes the regenerative responses to genetic manipulations of positional identity in the leg disc.

Fig. 1

(a–b) leg imaginal discs with anterior to the left and dorsal up. (a) schematic picture of a leg imaginal disc; (b) production of both bmp/dpp (green) and wg (red). The line indicates the x-axis of the proposed model.

Fig. 2

Sample graphs of the functions Act and Inh with m = 4, $u_0=\frac{1}{2}$, K_max = 1 and K_min = 0.

Fig. 3

Approximation of the heteroclinic connection for (17). For this simulation, I = 0.0099805992, m = 2, K_max = 0.051, K_min = 0.001. For these values, w₋ ~= 0.0000950097 and w₊ ~ 0.0075233436.

Fig. 4

Numerical simulation of full system with parameter values K_min = 0.0001 m = n = 3. In both runs the final time is t = 150000 seconds. The plots of w signal and b signal are plots of the production rates of w and b respectively.

Fig. 5

A numerical simulation of system (1) with m = 1, n = 3, K_min = 0.001 and K_max = 0.01. The final time step is at t = 100 seconds.

Fig. 6

A continuation of the simulation given in Figure 5 with a much larger time-step in order to display the convergence to an equilibrium. The final time step is at t = 5000 seconds.

Fig. 7

A numerical simulation of system (1) for m = 3, n = 3 and cross-inhibition of B_r on W shut off. The values of K_max and K_min are adjusted to produce maximum and minimum production rates of 0.01² and 0.001² respectively for all terms. Final time step is at t = 300 seconds.

Fig. 8

A continuation of the simulation given in Figure 7 with a much larger time-step in order to display the convergence to an equilibrium. Final time step is at t = 5000 seconds.

Fig. 9

A numerical simulation of system (1) for m = 3, n = 3 and auto-activation of W shut off. The values of K_max and K_min are adjusted to produce maximum and minimum production rates of 0.01² and 0.001² respectively for all terms. Final time step is at t = 300 seconds.

Fig. 10

A continuation of the simulation given in Figure 9 with a much larger time-step in order to display the convergence to an equilibrium. Final time step is at t = 5000 seconds.

Fig. 11

In this simulation there are no Wg receptors for 0.012 < x < 0.016 . The final time step is at t = 15000 seconds. The slight localized increase in W is due to lack of receptor to bind with. The localized increase in B is due to the local lack of inhibition.

Fig. 12

Simulation of region with defective Wg receptors in the region 0.013 < x < 0.018. Since Wg is still able to bind to its receptor there is no localized increase as seen in Figure 11. The final time step is at t = 15000 seconds. The experimental image is from [6].

Fig. 13

Simulation of region with Wg production set to its maximum rate independent of receptor binding for 0.012 < x < 0.016 causing localized increases in W and decreases in B. The final time step is at t = 15000 seconds. The experimental image from [6].