Decision making, movement planning and statistical decision theory
- PMID: 18614390
- PMCID: PMC2678412
- DOI: 10.1016/j.tics.2008.04.010
Decision making, movement planning and statistical decision theory
Abstract
We discuss behavioral studies directed at understanding how probability information is represented in motor and economic tasks. By formulating the behavioral tasks in the language of statistical decision theory, we can compare performance in equivalent tasks in different domains. Subjects in traditional economic decision-making tasks often misrepresent the probability of rare events and typically fail to maximize expected gain. By contrast, subjects in mathematically equivalent movement tasks often choose movement strategies that come close to maximizing expected gain. We discuss the implications of these different outcomes, noting the evident differences between the source of uncertainty and how information about uncertainty is acquired in motor and economic tasks.
Figures






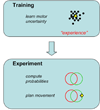

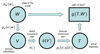
References
-
- Knill DC, Kersten D, Yuille A. Introduction: A Bayesian formulation of visual perception. In: Knill DC, Richards W, editors. Perception as Bayesian Inference. Cambridge University Press; New York: 1996. pp. 1–21.
-
- Landy MS, et al. Measurement and modeling of depth cue combination: in defense of weak fusion. Vis. Res. 1995;35(3):389–412. - PubMed
-
- Maloney LT. Statistical decision theory and biological vision. In: Heyer D, Mausfeld R, editors. Perception and the Physical World: Psychological and Philosophical Issues in Perception. Wiley; New York: 2002. pp. 145–189.
-
- Kahneman D, Tversky A. Choices, Values, and Frames. New York: Cambridge University Press; 2000. 840 pp. xx.
-
- Knight FH. Risk, Uncertainty and Profit. New York: Houghton Mifflin; 1921.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

