Stochastic simulation of enzyme-catalyzed reactions with disparate timescales

Abstract

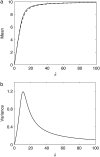
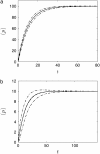
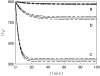
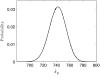
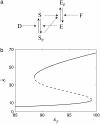
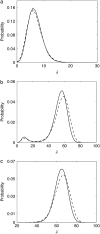
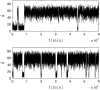
Many physiological characteristics of living cells are regulated by protein interaction networks. Because the total numbers of these protein species can be small, molecular noise can have significant effects on the dynamical properties of a regulatory network. Computing these stochastic effects is made difficult by the large timescale separations typical of protein interactions (e.g., complex formation may occur in fractions of a second, whereas catalytic conversions may take minutes). Exact stochastic simulation may be very inefficient under these circumstances, and methods for speeding up the simulation without sacrificing accuracy have been widely studied. We show that the "total quasi-steady-state approximation" for enzyme-catalyzed reactions provides a useful framework for efficient and accurate stochastic simulations. The method is applied to three examples: a simple enzyme-catalyzed reaction where enzyme and substrate have comparable abundances, a Goldbeter-Koshland switch, where a kinase and phosphatase regulate the phosphorylation state of a common substrate, and coupled Goldbeter-Koshland switches that exhibit bistability. Simulations based on the total quasi-steady-state approximation accurately capture the steady-state probability distributions of all components of these reaction networks. In many respects, the approximation also faithfully reproduces time-dependent aspects of the fluctuations. The method is accurate even under conditions of poor timescale separation.

FIGURE 1

Michaelis-Menten kinetics. (a) Comparison of steady-state mean of enzyme-substrate complex as a function of for The solid line plots calculated from the steady-state probability distribution, P(es), and the dashed line plots deterministic TQSSA results from Eq. 12. (b) Steady-state variance of the enzyme-substrate complex as a function of calculated from P(es).

FIGURE 2

Michaelis-Menten kinetics. Time evolution of mean product (solid line) ± 1 SD (dashed lines) calculated from the full Gillespie simulation. (a) and (b) and The lines for stochastic TQSSA simulations are indistinguishable from the full Gillespie simulations.

FIGURE 3

Goldbeter-Koshland switch. Time evolution of mean (solid line) ± 1 SD (dashed lines) for three different total numbers of enzyme molecules: (a) ; (b) ; and (c) Results of the full Gillespie and stochastic TQSSA simulations are indistinguishable.

FIGURE 4

Goldbeter-Koshland switch. Steady-state probability distributions of Ŝ_p for and The solid line represents the full Gillespie, and the dashed line the stochastic TQSSA.

FIGURE 5

Goldbeter-Koshland switch. Steady-state mean (bars) and standard deviation (error bars) of Ŝ_p (a) and D:S_p (b) for and The open bars represent the full Gillespie, and the hatched bars the stochastic TQSSA. In some cases, the standard deviations in stochastic TQSSA are so small that the error bars are not visible.

FIGURE 6

Goldbeter-Koshland switch. Autocorrelation functions of fluctuations for the species (a) Ŝ_p, (b) S_p, and (c) D:S_p, calculated from full Gillespie simulation (solid lines) and from stochastic TQSSA simulation (dashed lines) for different numbers of enzymes: (black); (red); and (blue).

FIGURE 7

Bistability for coupled GK switches. (a) Reaction scheme. (b) Bifurcation diagram.

FIGURE 8

Bistable switch. Steady-state probability distributions of Ŝ. The solid lines represent the full Gillespie, and the dashed line the stochastic TQSSA. (a) (b) and (c)

FIGURE 9

Bistable switch. The trajectory of Ŝ in the bistable zone (). (Upper) Full Gillespie simulation. (Lower) Stochastic TQSSA simulation.

FIGURE 10

Bistable switch. Plot of cumulative probability (p_t) of residence times (t_R) for (Upper) Upper steady state. (Lower) Lower steady state. The labeled lines represent full Gillespie (a), and stochastic TQSSA (b). Dashed lines are best-fitting exponential curves to the cumulative probability distributions.