Growth based morphogenesis of vertebrate limb bud

Abstract

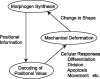
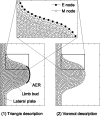
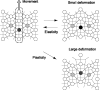
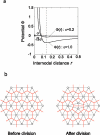
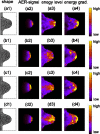
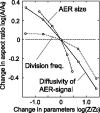
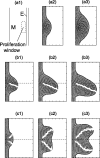
Many genes and their regulatory relationships are involved in developmental phenomena. However, by chemical information alone, we cannot fully understand changing organ morphologies through tissue growth because deformation and growth of the organ are essentially mechanical processes. Here, we develop a mathematical model to describe the change of organ morphologies through cell proliferation. Our basic idea is that the proper specification of localized volume source (e.g., cell proliferation) is able to guide organ morphogenesis, and that the specification is given by chemical gradients. We call this idea "growth-based morphogenesis." We find that this morphogenetic mechanism works if the tissue is elastic for small deformation and plastic for large deformation. To illustrate our concept, we study the development of vertebrate limb buds, in which a limb bud protrudes from a flat lateral plate and extends distally in a self-organized manner. We show how the proportion of limb bud shape depends on different parameters and also show the conditions needed for normal morphogenesis, which can explain abnormal morphology of some mutants. We believe that the ideas shown in the present paper are useful for the morphogenesis of other organs.

Fig. 1

Scheme of developmental dynamics. Organ morphogenesis is carried out through the interaction of several different processes, including the synthesis of morphogen at organ boundary, the decoding of positional information provided by the morphogen in cells, and the deformation and growth of the organ caused as a result of different cellular responses.

Fig. 2

(1) A network of nodes to describe the epithelial and mesenchymal tissues. The network composed of E- and M-nodes is constructed by the Delaunay triangulation. (2) Volonoi description of organ. The upper figure is a magnified view of a part in (1) and (2). Black and white nodes indicate E and M-nodes, respectively.

Fig. 3

Elastic and plastic properties of tissues. When the deformation of tissues through cell movement or division is small, the neighboring relationships among nodes remain unchanged. Thus, each node tries to restore equilibrium configuration (elasticity). In contrast, when the deformation is large, the neighboring relationships change and the shape would not return to the original one (plasticity). See the text for details.

Fig. 4

(a) Internodal potential energy Φ ^kl(k, l ∈ {M,E}). Φ ^kl is a function of the internodal distance r. Parameters ɛ and σ determine the magnitude of energy gradient and equilibrium distance between linked nodes, respectively. (b) Scheme of cell division. The left is a nodal network before cell division, and the right is one just after division (center cell). In both cases, the broken lines show the Delaunay triangulation and the red solid lines are the Voronoi partition.

Fig. 5

Temporal changes in the shape of a growing limb bud. (b–d) A limb bud protrudes from a flat lateral plate shown in (a), and extends with a constant width (e–g) in a self-organized manner (the time passes in an alphabet order). Pr: proximal, Di: distal, An: anterior, and Po: posterior. Parameter values: ɛ ^EE = 1.44, ɛ ^MM = 0.08, ɛ ^EM = 0.4, σ ^EE = 0.809, σ ^MM = 0.809, σ ^EM = 0.104, D = 0.15, γ = 0.10, μ = 3.3, f _div = 0.0033, c ^AER = 1.0, N _AER = 7.

Fig. 6

From the left to the right: organ shapes, distribution of AER-signal, energy level, and energy gradient in a transient state. Bright colors indicate high values. (a) Reference with a standard parameters set. (b) Case with a larger AER size. (c) Case with a higher diffusivity of the AER-signal. (d) Case with a higher division rate of M-nodes. The distributions of the AER-signal, energy level, and energy gradient are obtained as follows: first, we divided the region into small rectangular mashes. Then for each mesh, the averages of the AER-signal, energy level, and energy gradient over nodes included in the mesh are calculated.

Fig. 7

Parameter dependence of a limb bud shape at the final state. For all parameters to specify the spatio-temporal pattern of active proliferation area, such as AER size, diffusivity of AER-signal, expression level of AER-signal at AER, and division frequency of M-nodes, the dependence of the shape is qualitatively same. The shape becomes narrower and longer as each parameter decreases, while becomes wider and shorter as it increases. The figures (a)–(c) show the cases when only the AER-size is changed with all the other parameters fixed (the same as in Fig. 5). (a) N _AER = 3, (b) N _AER = 7 (reference), and (c) N _AER = 11.

Fig. 8

Parameters dependence of the aspect ratio, length/width. The horizontal axis indicates each parameter value normalized by its standard value; the vertical axis indicates the aspect ratio normalized by its value for the standard parameters set. Both are in a logarithmic plot. The aspect ratio monotonically decreases with the increase of parameters; AER size, diffusivity of AER-signal, and division frequency of M-nodes. Z: parameter value, Z ₀: parameter value for the reference, A: aspect ratio, A ₀: aspect ratio for the reference.

Fig. 9

Morphological anomalies. When the ratio of elasticity in epithelium to that in mesenchyme ɛ ^EE/ɛ ^MM is small, the surface of limb bud becomes rugged. On the other hand, when the ratio is large, the limb bud is hard to elongate distally and becomes balloon-like finally. The values of ɛ ^EE/ɛ ^MM are, from the left, 4.5, 18, and 90.

Fig. 10

(a) Temporal change in limb bud shape. (a1) The area in which M-nodes proliferate, which is fixed during development. Although a small hump protrudes from the flat lateral plate in the early phase (a2), the shape becomes more balloon-like with time (a3). (b) Temporal change in limb bud shape when the AER shifts toward the posterior direction. (b1–b3) Tissue growth tracks the trajectory of the AER (indicated by the white line), which leads to the shape of the limb bud that bends toward posterior direction. (c) Temporal change in limb bud shape when the AER bifurcates. (c1–c3) Tissue growth tracks the trajectory of the divided AERs (indicated by the white lines), which leads to a branched limb bud.