An MCMC algorithm for haplotype assembly from whole-genome sequence data
- PMID: 18676820
- PMCID: PMC2493424
- DOI: 10.1101/gr.077065.108
An MCMC algorithm for haplotype assembly from whole-genome sequence data
Abstract
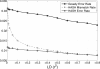
In comparison to genotypes, knowledge about haplotypes (the combination of alleles present on a single chromosome) is much more useful for whole-genome association studies and for making inferences about human evolutionary history. Haplotypes are typically inferred from population genotype data using computational methods. Whole-genome sequence data represent a promising resource for constructing haplotypes spanning hundreds of kilobases for an individual. In this article, we propose a Markov chain Monte Carlo (MCMC) algorithm, HASH (haplotype assembly for single human), for assembling haplotypes from sequenced DNA fragments that have been mapped to a reference genome assembly. The transitions of the Markov chain are generated using min-cut computations on graphs derived from the sequenced fragments. We have applied our method to infer haplotypes using whole-genome shotgun sequence data from a recently sequenced human individual. The high sequence coverage and presence of mate pairs result in fairly long haplotypes (N50 length ~ 350 kb). Based on comparison of the sequenced fragments against the individual haplotypes, we demonstrate that the haplotypes for this individual inferred using HASH are significantly more accurate than the haplotypes estimated using a previously proposed greedy heuristic and a simple MCMC method. Using haplotypes from the HapMap project, we estimate the switch error rate of the haplotypes inferred using HASH to be quite low, ~1.1%. Our Markov chain Monte Carlo algorithm represents a general framework for haplotype assembly that can be applied to sequence data generated by other sequencing technologies. The code implementing the methods and the phased individual haplotypes can be downloaded from (http://www.cse.ucsd.edu/users/vibansal/HASH/).
Figures


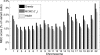

References
-
- Bafna V., Istrail S., Lancia G., Rizzi R., Istrail S., Lancia G., Rizzi R., Lancia G., Rizzi R., Rizzi R. Polynomial and APX-hard cases of individual haplotyping problems. Theor. Comput. Sci. 2005;335:109–125.
-
- Bentley D. Whole-genome re-sequencing. Curr. Opin. Genet. Dev. 2006;16:545–552. - PubMed
-
- Churchill G.A., Waterman M.S., Waterman M.S. The accuracy of dna sequences: Estimating sequence quality. Genomics. 1992;14:89–98. - PubMed
-
- Clark A.G. Inference of haplotypes from PCR-amplified samples of diploid populations. Mol. Biol. Evol. 1990;7:111–122. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
