Influence of nonlinear electrostatics on transfer energies between liquid phases: charge burial is far less expensive than Born model
- PMID: 18678891
- PMCID: PMC2516240
- DOI: 10.1073/pnas.0804506105
Influence of nonlinear electrostatics on transfer energies between liquid phases: charge burial is far less expensive than Born model
Abstract
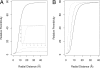
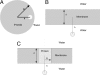
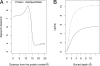
The widely used Born model describes the electrostatic response of continuous media using static dielectric constants. However, when applied to a liquid environment, a comparison of Born model predictions with experimental values (e.g., transfer free energies and pK(a) shifts) found that agreement is only achieved by using physically unrealistic dielectric constants for proteins, lipids, etc., and/or equally unrealistic atomic radii. This leads to questions concerning the physical origins for this failure of the Born model. We partially resolve this question by applying the Langevin-Debye (LD) model of a continuous distribution of point, polarizable dipoles, a model that contains an added dependence of the electrostatic response on the solvent's optical dielectric constant and both gas- and liquid-phase dipole moments, features absent in the Born model to which the LD model reduces for weak fields. The LD model is applied to simple representations of three biologically relevant systems: (i) globular proteins, (ii) lipid bilayers, and (iii) membrane proteins. The linear Born treatment greatly overestimates both the self-energy and the transfer free energy from water to hydrophobic environments (e.g., a protein interior). By using the experimental dielectric constant, the energy cost of charge burial in either globular or membrane proteins of the Born model is reduced by almost 50% with the nonlinear theory as is the pK(a) shift, and the shifts agree well with experimental trends.
Conflict of interest statement
The authors declare no conflict of interest.
Figures



Similar articles
-
Molecular dynamics simulations of a DMPC bilayer using nonadditive interaction models.Biophys J. 2009 Jan;96(2):385-402. doi: 10.1016/j.bpj.2008.09.048. Biophys J. 2009. PMID: 19167291 Free PMC article.
-
Revisiting the hexane-water interface via molecular dynamics simulations using nonadditive alkane-water potentials.J Chem Phys. 2006 May 28;124(20):204706. doi: 10.1063/1.2198538. J Chem Phys. 2006. PMID: 16774363
-
Binding of small basic peptides to membranes containing acidic lipids: theoretical models and experimental results.Biophys J. 1996 Aug;71(2):561-75. doi: 10.1016/S0006-3495(96)79280-9. Biophys J. 1996. PMID: 8842196 Free PMC article.
-
What are the dielectric "constants" of proteins and how to validate electrostatic models?Proteins. 2001 Sep 1;44(4):400-17. doi: 10.1002/prot.1106. Proteins. 2001. PMID: 11484218 Review.
-
Lipid bilayers: an essential environment for the understanding of membrane proteins.Magn Reson Chem. 2007 Dec;45 Suppl 1:S2-11. doi: 10.1002/mrc.2077. Epub 2007 Dec 19. Magn Reson Chem. 2007. PMID: 18095258 Review.
Cited by
-
HDX-MS performed on BtuB in E. coli outer membranes delineates the luminal domain's allostery and unfolding upon B12 and TonB binding.Proc Natl Acad Sci U S A. 2022 May 17;119(20):e2119436119. doi: 10.1073/pnas.2119436119. Epub 2022 May 12. Proc Natl Acad Sci U S A. 2022. PMID: 35549554 Free PMC article.
-
A Membrane Burial Potential with H-Bonds and Applications to Curved Membranes and Fast Simulations.Biophys J. 2018 Nov 20;115(10):1872-1884. doi: 10.1016/j.bpj.2018.10.012. Epub 2018 Oct 23. Biophys J. 2018. PMID: 30413241 Free PMC article.
-
Simple physics-based analytical formulas for the potentials of mean force of the interaction of amino-acid side chains in water. V. Like-charged side chains.J Phys Chem B. 2011 May 19;115(19):6119-29. doi: 10.1021/jp111258p. Epub 2011 Apr 18. J Phys Chem B. 2011. PMID: 21500792 Free PMC article.
-
Communication: modeling charge-sign asymmetric solvation free energies with nonlinear boundary conditions.J Chem Phys. 2014 Oct 7;141(13):131103. doi: 10.1063/1.4897324. J Chem Phys. 2014. PMID: 25296776 Free PMC article.
-
Ionic strength independence of charge distributions in solvation of biomolecules.J Chem Phys. 2014 Dec 14;141(22):22D503. doi: 10.1063/1.4895522. J Chem Phys. 2014. PMID: 25494774 Free PMC article.
References
-
- Warshel A, et al. Modeling electrostatic effects in proteins. Biochim Biophys Acta. 2006;1764:1647–1676. - PubMed
-
- Cramer CJ, Truhlar DG. Implicit solvation models: Equilibria, structure, spectra, and dynamics. Chem Rev. 1999;99:2161–2200. - PubMed
-
- Sandberg L, Edholm O. Nonlinear response effects in continuum models of the hydration of ions. J Chem Phys. 2002;116:2936–2944.
-
- Gilson MK, Honig BH. The dielectric constant of a folded protein. Biopolymers. 1986;25:2097–2119. - PubMed
-
- Bone S, Pethig R. Dielectric studies of the binding of water to lysozyme. J Mol Biol. 1982;157:571–575. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials

