Simulated two-dimensional red blood cell motion, deformation, and partitioning in microvessel bifurcations

Abstract

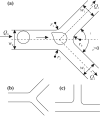
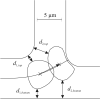
Movement, deformation, and partitioning of mammalian red blood cells (RBCs) in diverging microvessel bifurcations are simulated using a two-dimensional, flexible-particle model. A set of viscoelastic elements represents the RBC membrane and the cytoplasm. Motion of isolated cells is considered, neglecting cell-to-cell interactions. Center-of-mass trajectories deviate from background flow streamlines due to migration of flexible cells towards the mother vessel centerline upstream of the bifurcation and due to flow perturbations caused by cell obstruction in the neighborhood of the bifurcation. RBC partitioning in the bifurcation is predicted by determining the RBC fraction entering each branch, for a given partition of total flow and for a given upstream distribution of RBCs. Typically, RBCs preferentially enter the higher-flow branch, leading to unequal discharge hematocrits in the downstream branches. This effect is increased by migration toward the centerline but decreased by the effects of obstruction. It is stronger for flexible cells than for rigid circular particles of corresponding size, and decreases with increasing parent vessel diameter. For unequally sized daughter vessels, partitioning is asymmetric, with RBCs tending to enter the smaller vessel. Partitioning is not significantly affected by branching angles. Model predictions are consistent with previous experimental results.

Figure 1

(a) Schematic view of the two-dimensional model for a RBC. Rectangles denote viscoelastic/viscous elements of variable length, connected at the nodes. (b) Stresses and moments acting on node i.

Figure 2

Bifurcation geometries used. (a) Symmetric bifurcation with β₁ = β₂ = π/4 and r_d = w₁/w₂ = 1. (b) Bifurcation with asymmetric daughter vessel sizes; β₁ = β₂ = π/4 and r_d = 3^⅓ ≈ 1.44. (c) Bifurcation with asymmetric branching angles; β₁ = π/2, β₂ = 0, and r_d = 1.

Figure 3

(a) Example of center-of-mass trajectory, computed cell shapes and individual nodal velocities (arrows). Here Q₀ = 8 μm²/ms, w₀ = 8 μm, ψ₁ = ¼. Cell shapes are shown at t = 0, 10, and 30 ms. Dashed ellipse indicates cell in sandbag-like shape, adjacent to the flow divider. (b) Photomicrograph of RBCs in a capillary bifurcation in the rat mesentery. Scale is as in (a). One cell (indicated by dashed ellipse) is deformed into a sandbag-like shape, corresponding to the computed shape in (a). (c) Computed cell (solid) and underlying fluid (dashed) streamlines for the same geometry and ψ₁ = ¼. The dashed line that intersects the far wall of the bifurcation is the separating fluid streamline.

Figure 4

Separating streamlines and partitioning in symmetric bifurcations. (a,d) w₀ = 8 μm. (b,e) w₀ = 10.08 μm. (c,f) w₀ = 12.80 μm. (a,b,c) Initial positions of cells corresponding to separating flexible cell streamlines (solid), initial positions corresponding to separating rigid particle streamlines (long dashed), and y-coordinate which the underlying separating fluid streamline (short dashed) passes through at x = x₀. (d,e,f) Estimates for fractional RBC flux, Φ₁, as a function of fractional blood flow rate, ψ₁. The cell-free layers used for the rigid particle (long dashed) and flexible cell (solid) estimates are CFL = 0, 0.1 and 0.3 μm in (d,e,f). Short dashed lines are experimental estimates from.

Figure 5

(a) Comparison of results for symmetric bifurcations (solid) and bifurcations with asymmetric vessel diameters (dashed) for w₀ = 8 μm. Curves for the asymmetric bifurcation are shifted to the right. (b) Computed difference ΔΦ₁ between results for symmetric and asymmetric cases (solid curve) and estimated from empirical function (dotted curve).

Figure 6

Comparison of results from symmetric bifurcations (solid) with results from bifurcations with asymmetric branching angles (dashed). (a) Initial position x₀ = −15 μm. (b) Initial position x₀ = −20 μm in T-bifurcation, x₀ = −15 μm in symmetric bifurcation.

Figure 7

Computed RBC shapes in a T-bifurcation, showing asymmetry of fluid streamline (solid line) and of gaps on either side of the RBC.