New time-scale criteria for model simplification of bio-reaction systems

Abstract

Background: Quasi-steady state approximation (QSSA) based on time-scale analysis is known to be an effective method for simplifying metabolic reaction system, but the conventional analysis becomes time-consuming and tedious when the system is large. Although there are automatic methods, they are based on eigenvalue calculations of the Jacobian matrix and on linear transformations, which have a high computation cost. A more efficient estimation approach is necessary for complex systems.

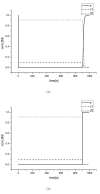
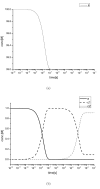
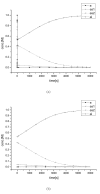
Results: This work derived new time-scale factor by focusing on the problem structure. By mathematically reasoning the balancing behavior of fast species, new time-scale criteria were derived with a simple expression that uses the Jacobian matrix directly. The algorithm requires no linear transformation or decomposition of the Jacobian matrix, which has been an essential part for previous automatic time-scaling methods. Furthermore, the proposed scale factor is estimated locally. Therefore, an iterative procedure was also developed to find the possible multiple boundary layers and to derive an appropriate reduced model.

Conclusion: By successive calculation of the newly derived time-scale criteria, it was possible to detect multiple boundary layers of full ordinary differential equation (ODE) models. Besides, the iterative procedure could derive the appropriate reduced differential algebraic equation (DAE) model with consistent initial values, which was tested with simple examples and a practical example.

Figure 1

Simplification results (I). Concentrations of e, c₁, and c₂ for the Michaelis-Menten system; (a) full ODE model solution and (b) reduced model solution.

Figure 2

Existence of multiple boundary layers. (a) Semi-log plot of s and (b) that of e, c₁, and c₂ for the Michaelis-Menten system. The existence of two boundary layers at the initial region are observed.

Figure 3

Simplification results (II). Concentrations of e, es₁, es₂, and ei for the Michaelis-Menten system with inhibition; (a) full ODE model solution and (b) reduced model solution.

Figure 4

Simplification results (III). Concentrations of c8 and c8* for the caspase system; (a) the solution profile of c8, from the full ODE model (c8) and from the reduced model (c8_red) and (b) the solution profile of c8*, from the full ODE model (c8*) and from the reduced model (c8*_red).