Complex ecological dynamics and eradicability of the vector borne macroparasitic disease, lymphatic filariasis

Abstract

Background: The current global efforts to control the morbidity and mortality caused by infectious diseases affecting developing countries--such as HIV/AIDS, polio, tuberculosis, malaria and the Neglected Tropical Diseases (NTDs)-have led to an increasing focus on the biological controllability or eradicability of disease transmission by management action. Here, we use an age-structured dynamical model of lymphatic filariasis transmission to show how a quantitative understanding of the dynamic processes underlying infection persistence and extinction is key to evaluating the eradicability of this macroparasitic disease.

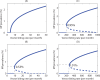
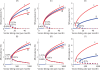
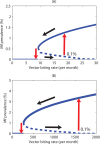
Methodology/principal findings: We investigated the persistence and extinction dynamics of lymphatic filariasis by undertaking a numerical equilibrium analysis of a deterministic model of parasite transmission, based on varying values of the initial L3 larval density in the system. The results highlighted the likely occurrence of complex dynamics in parasite transmission with three major outcomes for the eradicability of filariasis. First, both vector biting and worm breakpoint thresholds are shown to be complex dynamic entities with values dependent on the nature and magnitude of vector-and host specific density-dependent processes and the degree of host infection aggregation prevailing in endemic communities. Second, these thresholds as well as the potential size of the attractor domains and hence system resilience are strongly dependent on peculiarities of infection dynamics in different vector species. Finally, the existence of multiple stable states indicates the presence of hysteresis nonlinearity in the filariasis system dynamics in which infection thresholds for infection invasion are lower but occur at higher biting rates than do the corresponding thresholds for parasite elimination.

Conclusions/significance: The variable dynamic nature of thresholds and parasite system resilience reflecting both initial conditions and vector species-infection specificities, and the existence of hysteresis loop phenomenon, suggests that eradication of filariasis may require taking a more flexible and locally relevant approach to designing elimination programmes compared to the current command and control approach advocated by the global programme.

Figure 1. Functional forms relating microfilaria (Mf) uptake (from 20 µL host blood) and L3 development per mosquito in each vector genus.

The squares denote observed data for each vector respectively (sources outlined in the text). The curve fitted to the (A) Culex data is a limiting function of Mf (equation 6 in the text) whereas the Anopheles curve in (B) describes a development response that begins with a facilitation phase which then approaches an upper limit at higher Mf uptakes (equation 9 in the text).

Figure 2. The effect of varying the vector biting rate on the equilibrium Mf prevalence among human hosts when the vector intermediate host was culicine and when the worm mating probability was (A) and was not (B) included in the model, and when the intermediate host was anopheline with (C) no mating and with (D) mating probabilities included.

Inclusion of the mating probability introduced a set of breakpoints (dotted line) in the case of Culex, and it raised and increased the range of the breakpoints in the case of Anopheles. The labelled Mf values on the y-axes correspond to the maximum breakpoints, whereas additionally in each graph the solid curve (A) and vertical dashed drop lines (B–D) crossing the x-axes denote the threshold biting rates (TBRs) estimated in each scenario corresponding to A) 4, B) 9, C) 197, D) 271 vector bites per month.

Figure 3. The direction of change of the Mf prevalence age-profile among human hosts when the intermediate host was culicine and the initial Mf prevalence was (A) above and (B) below the breakpoint value (0.21%) with a vector biting rate of 11 per month; and when the intermediate host was anopheline with initial Mf prevalence (C) above and (D) below the breakpoint value (0.82%) with a vector biting rate of 280 per month.

Each age-dependent curve represents a perturbation around the initial unstable equilibrium curve with the black arrows indicating the direction in which these curves are likely to travel on the way to the stable equilibrium.

Figure 4. The direction of change of the Mf prevalence age-profile among human hosts at different anopheline vector biting rates.

Results are shown for vector biting rates of (A) 280 (just above the TBR of 271), (B) 350, and (C) 600. In each case, the blue curves represent initial perturbations around the Mf age-profile corresponding to the breakpoint Mf prevalence (red curve), and the black arrows indicate the direction in which the curves are likely to travel on the way to attaining the zero or endemic stable equilibrium.

Figure 5. Sensitivity of the endemic Mf prevalence, breakpoint values, and TBRs to changes in the shape parameter of the negative binomial distribution, (k) describing the distribution of Mf among human hosts ((A) and (B)), the strength of the immune response to infection, β ((C) and (D)), and per capita worm fecundity, α ((E) and (F)).

The k values were varied by maintaining the linear dependence upon Mf values (see text) but increasing/decreasing the linear component by 50% so that this value was given by i) 0.0354, ii) 0.0236, and iii) 0.0118. When the intermediate host was (A) culicine, the maximum value of the breakpoint changed with k, but the TBR (units are bites per month) did not change (TBR = 9). For anopheline intermediate hosts (B), both the maximum breakpoint and the TBR decreased with decreasing k (TBR = i) 306, ii) 271, iii) 233)). The parameter β can be thought of as an index governing the strength of the density dependent establishment of parasites in the human hosts. The β values were varied by 10% so that the values used here were: i) 0.1, ii) 0.112, and iii) 0.122. When the intermediate host was (C) culicine, the maximum value of the breakpoint changed with β, but the TBR did not change from its value of 9. For anopheline intermediate hosts (D), the maximum breakpoint decreased and the TBR increased with increasing β (decreasing density dependence) (TBR = i) 252, ii) 271, iii) 285)). Graphs (E) and (F) depict the steady state Mf prevalence values found for values of per capita worm fecundity, α, of either i) 0.4 or ii) 0.2. When the intermediate host was either (E) culicine or (F) anopheline, the maximum value of the breakpoint rose and the TBR was lowered with increasing α (TBR (E) Culex: i) 5, ii) 9; (F) Anopheles: i) 104, ii) 271)).

Figure 6. Hysteresis loops in the Mf prevalence/vector biting rate plane for (A) culicine and (B) anopheline intermediate hosts, showing the two asymmetrical ways by which a shift between alternative Mf stable states can occur with varying vector biting rates.

If the parasite system is on the lower zero state but at high vector biting rates and thus close to the worm breakpoint bifurcation boundary, a slight incremental change in Mf levels may bring it beyond the birfurcation (say at 0.1% Mf prevalence) and induce a drastic shift of the system to its endemic equilibrium (rightmost red arrow). If one attempts to restore the parasite-free equilibrium state by reducing the vector biting rate (black leftward arrow), the system shows hysteresis. A backward shift to the parasite-free equilibrium (leftmost red arrow) will occur only if the vector biting rate is reduced far enough to reach the TBR bifurcation point. The hysteresis loop is wider in extent for the anopheline model compared to culicine-transmitted filariasis.