Potential landscape and flux framework of nonequilibrium networks: robustness, dissipation, and coherence of biochemical oscillations
- PMID: 18719111
- PMCID: PMC2527901
- DOI: 10.1073/pnas.0800579105
Potential landscape and flux framework of nonequilibrium networks: robustness, dissipation, and coherence of biochemical oscillations
Abstract
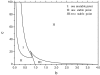
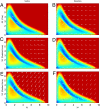
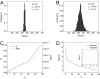
We established a theoretical framework for studying nonequilibrium networks with two distinct natures essential for characterizing the global probabilistic dynamics: the underlying potential landscape and the corresponding curl flux. We applied the idea to a biochemical oscillation network and found that the underlying potential landscape for the oscillation limit cycle has a distinct closed ring valley (Mexican hat-like) shape when the fluctuations are small. This global landscape structure leads to attractions of the system to the ring valley. On the ring, we found that the nonequilibrium flux is the driving force for oscillations. Therefore, both structured landscape and flux are needed to guarantee a robust oscillating network. The barrier height separating the oscillation ring and other areas derived from the landscape topography is shown to be correlated with the escaping time from the limit cycle attractor and provides a quantitative measure of the robustness for the network. The landscape becomes shallower and the closed ring valley shape structure becomes weaker (lower barrier height) with larger fluctuations. We observe that the period and the amplitude of the oscillations are more dispersed and oscillations become less coherent when the fluctuations increase. We also found that the entropy production of the whole network, characterizing the dissipation costs from the combined effects of both landscapes and fluxes, decreases when the fluctuations decrease. Therefore, less dissipation leads to more robust networks. Our approach is quite general and applicable to other networks, dynamical systems, and biological evolution. It can help in designing robust networks.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
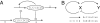





References
-
- Fall CP, Marland ES, Wagner JM, Tyson JJ. Computational Cell Biology. New York: Springer; 2002. Chap 9.
-
- Gillespie DT. Exact stochastic simulation of coupled chemical reactions. J Phys Chem. 1977;81:2340–2361.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Molecular Biology Databases

