Low-frequency envelope sensitivity produces asymmetric binaural tuning curves
- PMID: 18753329
- PMCID: PMC2576218
- DOI: 10.1152/jn.90393.2008
Low-frequency envelope sensitivity produces asymmetric binaural tuning curves
Abstract
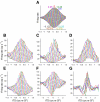
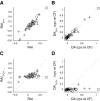
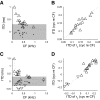
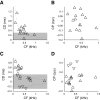
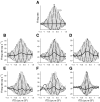
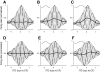
Neurons in the auditory midbrain are sensitive to differences in the timing of sounds at the two ears--an important sound localization cue. We used broadband noise stimuli to investigate the interaural-delay sensitivity of low-frequency neurons in two midbrain nuclei: the inferior colliculus (IC) and the dorsal nucleus of the lateral lemniscus. Noise-delay functions showed asymmetries not predicted from a linear dependence on interaural correlation: a stretching along the firing-rate dimension (rate asymmetry), and a skewing along the interaural-delay dimension (delay asymmetry). These asymmetries were produced by an envelope-sensitive component to the response that could not entirely be accounted for by monaural or binaural nonlinearities, instead indicating an enhancement of envelope sensitivity at or after the level of the superior olivary complex. In IC, the skew-like asymmetry was consistent with intermediate-type responses produced by the convergence of ipsilateral peak-type inputs and contralateral trough-type inputs. This suggests a stereotyped pattern of input to the IC. In the course of this analysis, we were also able to determine the contribution of time and phase components to neurons' internal delays. These findings have important consequences for the neural representation of interaural timing differences and interaural correlation-cues critical to the perception of acoustic space.
Figures

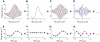



Similar articles
-
Interaural delay sensitivity and the classification of low best-frequency binaural responses in the inferior colliculus of the guinea pig.Hear Res. 1996 Aug;97(1-2):136-52. Hear Res. 1996. PMID: 8844194
-
Slow Temporal Integration Enables Robust Neural Coding and Perception of a Cue to Sound Source Location.J Neurosci. 2016 Sep 21;36(38):9908-21. doi: 10.1523/JNEUROSCI.1421-16.2016. J Neurosci. 2016. PMID: 27656028 Free PMC article.
-
Tuning to interaural time difference and frequency differs between the auditory arcopallium and the external nucleus of the inferior colliculus.J Neurophysiol. 2009 May;101(5):2348-61. doi: 10.1152/jn.91196.2008. Epub 2009 Mar 4. J Neurophysiol. 2009. PMID: 19261709
-
Circuits for processing dynamic interaural intensity disparities in the inferior colliculus.Hear Res. 2012 Jun;288(1-2):47-57. doi: 10.1016/j.heares.2012.01.011. Epub 2012 Feb 8. Hear Res. 2012. PMID: 22343068 Free PMC article. Review.
-
Monaural and binaural processing in the ventral nucleus of the lateral lemniscus: a major source of inhibition to the inferior colliculus.Hear Res. 2002 Jun;168(1-2):90-7. doi: 10.1016/s0378-5955(02)00368-4. Hear Res. 2002. PMID: 12117512 Review.
Cited by
-
Neural coding of dichotic pitches in auditory midbrain.J Neurophysiol. 2023 Apr 1;129(4):872-893. doi: 10.1152/jn.00511.2022. Epub 2023 Mar 15. J Neurophysiol. 2023. PMID: 36921210 Free PMC article.
-
Transformation from a pure time delay to a mixed time and phase delay representation in the auditory forebrain pathway.J Neurosci. 2012 Apr 25;32(17):5911-23. doi: 10.1523/JNEUROSCI.5429-11.2012. J Neurosci. 2012. PMID: 22539852 Free PMC article.
-
A mammalian inferior colliculus model for sound source separation using interaural time differences.PLoS Comput Biol. 2025 Jun 24;21(6):e1013243. doi: 10.1371/journal.pcbi.1013243. eCollection 2025 Jun. PLoS Comput Biol. 2025. PMID: 40554588 Free PMC article.
-
Frequency-invariant representation of interaural time differences in mammals.PLoS Comput Biol. 2011 Mar;7(3):e1002013. doi: 10.1371/journal.pcbi.1002013. Epub 2011 Mar 17. PLoS Comput Biol. 2011. PMID: 21445227 Free PMC article.
-
Action potential generation in an anatomically constrained model of medial superior olive axons.J Neurosci. 2014 Apr 9;34(15):5370-84. doi: 10.1523/JNEUROSCI.4038-13.2014. J Neurosci. 2014. PMID: 24719114 Free PMC article.
References
-
- Adams JC, Mugnaini E. Dorsal nucleus of the lateral lemniscus: a nucleus of GABAergic projection neurons. Brain Res Bull 13: 585–590, 1984. - PubMed
-
- Albeck Y, Konishi M. Responses of neurons in the auditory pathway of the barn owl to partially correlated binaural signals. J Neurophysiol 74: 1689–1700, 1995. - PubMed
-
- Batra R, Kuwada S, Fitzpatrick DC. Sensitivity to interaural temporal disparities of low- and high-frequency neurons in the superior olivary complex. I. Heterogeneity of responses. J Neurophysiol 78: 1222–1236, 1997. - PubMed
-
- Batra R, Kuwada S, Stanford TR. High-frequency neurons in the inferior colliculus that are sensitive to interaural delays of amplitude-modulated tones: evidence for dual binaural influences. J Neurophysiol 70: 64–80, 1993. - PubMed
-
- Bernstein LR, Trahiotis C. Lateralization of low-frequency, complex waveforms: the use of envelope-based temporal disparities. J Acoust Soc Am 77: 1868–1880, 1985. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

