Genome-scale model for Clostridium acetobutylicum: Part II. Development of specific proton flux states and numerically determined sub-systems

Abstract

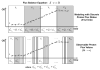
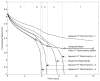
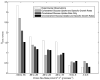
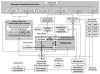
A regulated genome-scale model for Clostridium acetobutylicum ATCC 824 was developed based on its metabolic network reconstruction. To aid model convergence and limit the number of flux-vector possible solutions (the size of the phenotypic solution space), modeling strategies were developed to impose a new type of constraint at the endo-exo-metabolome interface. This constraint is termed the specific proton flux state, and its use enabled accurate prediction of the extracellular medium pH during vegetative growth of batch cultures. The specific proton flux refers to the influx or efflux of free protons (per unit biomass) across the cell membrane. A specific proton flux state encompasses a defined range of specific proton fluxes and includes all metabolic flux distributions resulting in a specific proton flux within this range. Effective simulation of time-course batch fermentation required the use of independent flux balance solutions from an optimum set of specific proton flux states. Using a real-coded genetic algorithm to optimize temporal bounds of specific proton flux states, we show that six separate specific proton flux states are required to model vegetative-growth metabolism and accurately predict the extracellular medium pH. Further, we define the apparent proton flux stoichiometry per weak acids efflux and show that this value decreases from approximately 3.5 mol of protons secreted per mole of weak acids at the start of the culture to approximately 0 at the end of vegetative growth. Calculations revealed that when specific weak acids production is maximized in vegetative growth, the net proton exchange between the cell and environment occurs primarily through weak acids efflux (apparent proton flux stoichiometry is 1). However, proton efflux through cation channels during the early stages of acidogenesis was found to be significant. We have also developed the concept of numerically determined sub-systems of genome-scale metabolic networks here as a sub-network with a one-dimensional null space basis set. A numerically determined sub-system was constructed in the genome-scale metabolic network to study the flux magnitudes and directions of acetylornithine transaminase, alanine racemase, and D-alanine transaminase. These results were then used to establish additional constraints for the genome-scale model.

Figure 1

Illustration of discretized and continuous proton flux states using fictitious optical density (OD) data. Specific proton flux values are represented by $q_{{\text{H}}_{\text{ext}}^{+}}^i$ and discrete proton flux states are represented by Q_i. The number of flux solutions, v, to the flux balance equation, S·v = 0, based on proton flux state, is represented by N.

Figure 2

Simple example of numerically defining a sub-system by resolving a singularity with a flux ratio relationship and applying kinetic parameters.

Figure 3

Raw data (circles) and optimized genome-scale model predictions (lines) for biomass production, glucose consumption, acids and solvents production during exponential growth of C. acetobutylicum on minimal media (Monot et al., 1982). The following model predictions are shown: (i) six discrete proton flux states (Set 3 of Table II) (solid lines) and (ii) single proton flux state model (Set 1 of Table II) (dashed lines). Note: experimental observations with minimal media were not reported for acetone; only model predictions are shown for this case.

Figure 4

Model-derived values (lines) and raw data points (circles) of extracellular media pH for batch growth of C. acetobutylicum in minimal media (Monot et al., 1982). Proton flux states are labeled by letters: (a) −100 to −55 mmol H⁺ h⁻¹ g biomass⁻¹, (b) −55 to −35 mmol H⁺ h⁻¹ g biomass⁻¹, (c) −35 to −25 mmol H⁺ h⁻¹ g biomass⁻¹, (d) −25 to −15 mmol H⁺ h⁻¹ g biomass⁻¹, (e) −15 to −5 mmol H⁺ h⁻¹ g biomass⁻¹, and (f) −5 to 5 mmol H⁺ h⁻¹ g biomass⁻¹. The Complete Model is composed of six discrete proton flux states with specific fluxes and growth rates shown in Table III and growth and metabolite predictions shown in this figure. The Single Flux State Model consists of a single proton flux state with growth and metabolite predictions shown in this figure. The Apparent H⁺ Stoichiometry curves correspond to specific fluxes in Table III with proton flux from cation transport reactions ignored. Stoichiometric coefficient for protons associated with acetate and butyrate efflux was adjusted from 1 to 4 and is listed for each case. The Fitted H⁺ Stoichiometry Model contains adjusted stoichiometric coefficients for proton efflux with weak acids to fit the observed extracellular medium pH profile.

Figure 5

Calculated specific growth rate for specified proton flux states given multiple values of the stoichiometry of ATP in the biomass constituting equation (Eq. 5). The dashed horizontal lines correspond to the experimentally observed specific growth rate (Monot et al., 1982). Numerical values printed above the data correspond to the optimized value of the stoichiometric coefficient of ATP (also referred to as γ in Eq. 5) for each proton flux state. Error bars are given for the case in which the stoichiometric coefficient of ATP is equal to 200 and represent one standard deviation.

Figure 6

The selectivity of acids to solvents for: (i) experimental observations, (ii) simulation of the genome-scale model in which glucose uptake and specific growth rates were constrained to experimentally observed values (Monot et al., 1982), (iii) simulations in which only the glucose uptake rate was constrained, and (iv) model simulations with no constraints on glucose uptake or specific growth rates. In all cases, reaction fluxes determining the proton flux state (including butyric, acetic, and lactic acids efflux) and solvent (acetone, butanol, and ethanol) effluxes were left unconstrained. The selectivity of acids to solvents is defined as the sum of butyric, acetic, and lactic acids efflux divided by the sum of acetone, butanol, and ethanol effluxes.

Figure 7

Sub-system of the genome-scale model to investigate flux constraint bounds around D-alanine and probe metabolic capacity based on its incorporation into D-alanylation of wall teichoic acids. The location of the singularity of the sub-system is identified. It was resolved by varying the ratio of Reaction 1 (through acetylornithine transaminase (ArgD, EC 2.6.1.11, CAC2388)) to Reaction 4 (L-glutamate biosynthesis through L-arginine biosynthesis pathway). Reaction 2 is catalyzed by the alanine racemace (EC 5.1.1.1, CAC0492) and D-alanine transaminase (EC 2.6.2.21, CAC0792) drives Reaction 3. Not present in the diagram above, but assumed to be available in excess were: (i) all L-amino acids not derived from L-glutamate, (ii) all required lipids for biomass synthesis, (iii) phosphorylated carbohydrate required by nucleotide biosynthesis, (iv) all intracellular solute pools, (v) sources of all additional molecules required by synthesis reactions, (vi) sinks for all byproducts of synthesis reactions and (vii) all energy requirements.

Figure 8

Results of simulations for the numerically defined sub-system shown in Figure 6. a: The flux ratio for L-glutamate production from ArgD to nitrogen assimilation (Reactions 1 and 4 in Fig. 6), was varied to produce ratios of the specific flux of L-alanine through alanine racemace (Reaction 2 in Fig. 6) against the flux of L-alanine through acetylornithine transaminase (Reaction 1 in Fig. 6). The simulation was performed for multiple assumed specific growth rates between 0.05 h⁻¹ and 0.35 h⁻¹. b: The relationship between the specific flux of D-alanine through D-alanine transaminase (Reaction 3 in Fig. 6) and the specific flux of L-alanine through acetylornithine transaminase (Reaction 1 in Fig. 6) was produced by varying the flux ratio for L-glutamate production. This is shown for an increasing number (0–50) of D-alanine residues involved in D-alanylation of wall teichoic acids. For these calculations, a specific growth rate of 0.3 h⁻¹ was assumed.