Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2008 Aug 28;3(8):e3079.
doi: 10.1371/journal.pone.0003079.

Entropy bounds for hierarchical molecular networks

Matthias Dehmer  1 , Stephan Borgert, Frank Emmert-Streib
Affiliations

Entropy bounds for hierarchical molecular networks

Matthias Dehmer et al. PLoS One. .

Abstract

In this paper we derive entropy bounds for hierarchical networks. More precisely, starting from a recently introduced measure to determine the topological entropy of non-hierarchical networks, we provide bounds for estimating the entropy of hierarchical graphs. Apart from bounds to estimate the entropy of a single hierarchical graph, we see that the derived bounds can also be used for characterizing graph classes. Our contribution is an important extension to previous results about the entropy of non-hierarchical networks because for practical applications hierarchical networks are playing an important role in chemistry and biology. In addition to the derivation of the entropy bounds, we provide a numerical analysis for two special graph classes, rooted trees and generalized trees, and demonstrate hereby not only the computational feasibility of our method but also learn about its characteristics and interpretability with respect to data analysis.

PubMed Disclaimer

Conflict of interest statement

Competing Interests: The authors have declared that no competing interests exist.

Figures

Figure 1
Figure 1. Overall approach to derive entropy bounds for hierarchical graphs.
Figure 2
Figure 2. G represents an undirected and connected graph.
For example, we get |S 1(vi,G)| = 5 and |S 2(vi,G)| = 9.
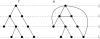
Figure 3
Figure 3. An undirected tree T and its corresponding undirected generalized tree H.
It holds |L| = 4 and h = |L|−1 = 3.
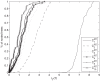
Figure 4
Figure 4. Cumulative entropy distributions of the classes CαRT for h = 8.
The x-axis corresponds to the entropy IfV (T) and the y-axis represents the cumulative entropy distribution for C 1 RT -C 5 RT and C 10 RT.
Figure 5
Figure 5. Cumulative entropy distributions of the classes CαGT for h = 8.
The x-axis corresponds to the entropy IfV (H) and the y-axis represents the cumulative entropy distribution for C 1 GT -C 5 GT and C 10 GT.
See this image and copyright information in PMC

References

    1. Bonchev D, Rouvray DH. Chemical Graph Theory. Introduction and Fundamentals. Abacus Press; 1991.
    1. Diudea MV, Gutman I, Jäntschi L. Molecular Topology. Nova Publishing; 2001.
    1. Gutman I, Polansky OE. Mathematical Concepts in Organic Chemistry. Springer; 1986.
    1. Trinajstić N. Chemical Graph Theory. CRC Press; 1992.
    1. Batagelj V. Graovac A, editor. Similarity measures between structured objects. Dubrovnik/Yugoslavia: Proceedings of an International Course and Conference on the Interfaces between Mathematics, Chemistry and Computer Sciences. 1988. pp. 25–40.