Multifinger prehension: an overview
- PMID: 18782719
- PMCID: PMC2659677
- DOI: 10.3200/JMBR.40.5.446-476
Multifinger prehension: an overview
Abstract
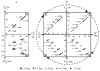
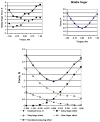
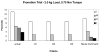
The authors review the available experimental evidence on what people do when they grasp an object with several digits and then manipulate it. The article includes three parts, each addressing a specific aspect of multifinger prehension. In the first part, the authors discuss manipulation forces (i.e., the resultant force and moment of force exerted on the object) and the digits' contribution to such forces' production. The second part deals with internal forces defined as forces that cancel each other and do not disturb object equilibrium. The authors discuss the role of the internal forces in maintaining the object stability, with respect to such issues as slip prevention, tilt prevention, and resistance to perturbations. The third part is devoted to the motor control of prehension. It covers such topics as prehension synergies, chain effects, the principle of superposition, interfinger connection matrices and reconstruction of neural commands, mechanical advantage of the fingers, and the simultaneous digit adjustment to several mutually reinforcing or conflicting demands.
Figures










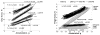
Similar articles
-
Stability of the multi-finger prehension synergy studied with transcranial magnetic stimulation.Exp Brain Res. 2008 Sep;190(2):225-38. doi: 10.1007/s00221-008-1466-x. Epub 2008 Jul 1. Exp Brain Res. 2008. PMID: 18592229 Free PMC article.
-
Digit force adjustments during finger addition/removal in multi-digit prehension.Exp Brain Res. 2008 Aug;189(3):345-59. doi: 10.1007/s00221-008-1430-9. Epub 2008 Jun 14. Exp Brain Res. 2008. PMID: 18553076 Free PMC article.
-
Adjustments of prehension synergies in response to self-triggered and experimenter-triggered load and torque perturbations.Exp Brain Res. 2006 Nov;175(4):641-53. doi: 10.1007/s00221-006-0583-7. Epub 2006 Jun 28. Exp Brain Res. 2006. PMID: 16804720 Free PMC article.
-
Prehension synergies.Exerc Sport Sci Rev. 2004 Apr;32(2):75-80. doi: 10.1097/00003677-200404000-00007. Exerc Sport Sci Rev. 2004. PMID: 15064652 Free PMC article. Review.
-
Multi-finger prehension: control of a redundant mechanical system.Adv Exp Med Biol. 2009;629:597-618. doi: 10.1007/978-0-387-77064-2_32. Adv Exp Med Biol. 2009. PMID: 19227523 Review.
Cited by
-
Grip-force modulation in multi-finger prehension during wrist flexion and extension.Exp Brain Res. 2013 Jun;227(4):509-22. doi: 10.1007/s00221-013-3527-z. Epub 2013 Apr 30. Exp Brain Res. 2013. PMID: 23625077 Free PMC article. Clinical Trial.
-
The synergic control of multi-finger force production: stability of explicit and implicit task components.Exp Brain Res. 2017 Jan;235(1):1-14. doi: 10.1007/s00221-016-4768-4. Epub 2016 Sep 6. Exp Brain Res. 2017. PMID: 27601252 Free PMC article.
-
Case Studies in Neuroscience: The central and somatosensory contributions to finger interdependence and coordination: lessons from a study of a "deafferented person".J Neurophysiol. 2019 Jun 1;121(6):2083-2087. doi: 10.1152/jn.00153.2019. Epub 2019 Apr 10. J Neurophysiol. 2019. PMID: 30969884 Free PMC article.
-
Force coordination in static manipulation tasks performed using standard and non-standard grasping techniques.Exp Brain Res. 2009 Apr;194(4):605-18. doi: 10.1007/s00221-009-1738-0. Epub 2009 Feb 27. Exp Brain Res. 2009. PMID: 19247643
-
Prehension synergies during fatigue of a single digit: adaptations in control with referent configurations.Motor Control. 2014 Jul;18(3):278-96. doi: 10.1123/mc.2013-0069. Epub 2014 Jan 21. Motor Control. 2014. PMID: 24457335 Free PMC article.
References
-
- Arbib MA, Iberall T, Lyons D. Coordinated control programs for movements of the hand. In: Goodwin AW, Darian-Smith I, editors. Hand Function and the Neocortex. Berlin: Springer Verlag; 1985. pp. 111–129.
-
- Arimoto S, Tahara K, Yamaguchi M, Nguyen PTA, Han HY. Principles of superposition for controlling pinch motions by means of robot fingers with soft tips. Robotica. 2001;19:21–28.
-
- Augurelle AS, Penta M, White O, Thonnard JL. The effects of a change in gravity on the dynamics of prehension. Experimental Brain Research. 2003a;148(4):533–40. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
