Inference for outcome probabilities in multi-state models
- PMID: 18791824
- PMCID: PMC2735091
- DOI: 10.1007/s10985-008-9097-x
Inference for outcome probabilities in multi-state models
Abstract
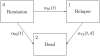
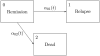
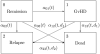
In bone marrow transplantation studies, patients are followed over time and a number of events may be observed. These include both ultimate events like death and relapse and transient events like graft versus host disease and graft recovery. Such studies, therefore, lend themselves for using an analytic approach based on multi-state models. We will give a review of such methods with emphasis on regression models for both transition intensities and transition- and state occupation probabilities. Both semi-parametric models, like the Cox regression model, and parametric models based on piecewise constant intensities will be discussed.
Figures













References
-
- Andersen PK, Hansen LS, Keiding N. Non- and semi-parametric estimation of transition probabilities from censored observation of a non-homogeneous Markov process. Scand J Stat. 1991;18:153–167.
-
- Andersen PK, Borgan Ø, Gill RD, Keiding N. Statistical models based on counting processes. Springer-Verlag; New York: 1993.
-
- Andersen PK, Keiding N. Multi-state models for event history analysis. Stat Methods Med Res. 2002;11:91–115. - PubMed
-
- Andersen PK, Klein JP. Regression analysis for multistate models based on a pseudo-value approach, with applications to bone marrow transplantation studies. Scand J Stat. 2007;34:3–16.
-
- Cheng SC, Fine JP, Wei LJ. Prediction of cumulative incidence function under the proportional hazards model. Biometrics. 1998;54:219–228. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Medical

