Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2008;95(2):307-323.
doi: 10.1093/biomet/asn012.

Kernel stick-breaking processes

David B Dunson  1 , Ju-Hyun Park
Affiliations

Kernel stick-breaking processes

David B Dunson et al. Biometrika. 2008.

Abstract

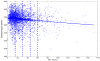
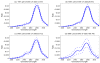
We propose a class of kernel stick-breaking processes for uncountable collections of dependent random probability measures. The process is constructed by first introducing an infinite sequence of random locations. Independent random probability measures and beta-distributed random weights are assigned to each location. Predictor-dependent random probability measures are then constructed by mixing over the locations, with stick-breaking probabilities expressed as a kernel multiplied by the beta weights. Some theoretical properties of the process are described, including a covariate-dependent prediction rule. A retrospective Markov chain Monte Carlo algorithm is developed for posterior computation, and the methods are illustrated using a simulated example and an epidemiological application.

PubMed Disclaimer

Figures

Fig. 1
Fig. 1
Results for the kernel stick-breaking reference analysis in the simulation example. Estimated conditional response densities are shown for different percentiles of the predictor, including (a) 10th, (b) 25th, (c) 50th, (d) 75th, (e) 90th. The raw data and mean regression estimator are shown in (f). The solid lines are the posterior means, the dashed lines are pointwise 99% credible intervals, and the dotted lines are the true values.
Fig. 2
Fig. 2
dde vs gestational age at delivery in days for 2313 women in the Longnecker et al. (2001) study. The solid line is the conditional predictive mean, while the dotted lines are 99% pointwise credible intervals. Vertical dashed lines are dde quintiles.
Fig. 3
Fig. 3
Estimated densities of gestational age at delivery (in days) conditionally on dde, f(y|x), for the kernel stick-breaking reference analysis. Estimates correspond to different percentiles of the predictor distribution, including (a) 10th, (b) 60th, (c) 90th and (d) 99th. Solid lines represent posterior means, and dashed lines represent 99% credible intervals.
Fig. 4
Fig. 4
Estimated probability gestational age at delivery is less than T weeks versus dde dose, for (a) T = 33, (b) T = 35, (c) T = 37, (d) T = 40. Solid lines are posterior means and dashed lines are pointwise 99% credible intervals.
See this image and copyright information in PMC

References

    1. ALDOUS DJ. Exchangeability and related topics. École d’ Été de Probabilités de Saint-Flour XII. In: Hennequin PL, editor. Springer Lecture Notes Math. Vol. 1117. Berlin: Springer; 1985. pp. 1–198.
    1. BLACKWELL D, MACQUEEN JB. Ferguson distributions via Pólya urn schemes. Ann Statist. 1973;1:353–5.
    1. BARRY D, HARTIGAN JA. Product partition models for change point problems. Ann Statist. 1992;20:260–79.
    1. CARON F, DAVY M, DOUCET A, DUFLOS E, VANHEEGHE P. Bayesian inference for dynamic models with Dirichlet process mixtures. International Conference on Information Fusion; Florence, Italy: INRIA - CCSd - CNRS. 2006. pp. 1–8.
    1. CIFARELLI DM, REGAZINNI E. Nonparametric statistical problems under partial exchangeability: The use of associative means. Ann Inst Mat Finian Univ Torino, II. 1978;12:1–36.