Toward realistic and practical ideal observer (IO) estimation for the optimization of medical imaging systems

Abstract

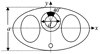
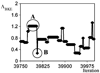
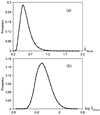
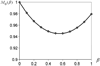
The ideal observer (IO) employs complete knowledge of the available data statistics and sets an upper limit on observer performance on a binary classification task. However, the IO test statistic cannot be calculated analytically, except for cases where object statistics are extremely simple. Kupinski have developed a Markov chain Monte Carlo (MCMC) based technique to compute the IO test statistic for, in principle, arbitrarily complex objects and imaging systems. In this work, we applied MCMC to estimate the IO test statistic in the context of myocardial perfusion SPECT (MPS). We modeled the imaging system using an analytic SPECT projector with attenuation, distant-dependent detector-response modeling and Poisson noise statistics. The object is a family of parameterized torso phantoms with variable geometric and organ uptake parameters. To accelerate the imaging simulation process and thus enable the MCMC IO estimation, we used discretized anatomic parameters and continuous uptake parameters in defining the objects. The imaging process simulation was modeled by precomputing projections for each organ for a finite number of discretely-parameterized anatomic parameters and taking linear combinations of the organ projections based on continuous sampling of the organ uptake parameters. The proposed method greatly reduces the computational burden and allows MCMC IO estimation for a realistic MPS imaging simulation. We validated the proposed IO estimation technique by estimating IO test statistics for a large number of input objects. The properties of the first- and second-order statistics of the IO test statistics estimated using the MCMC IO estimation technique agreed well with theoretical predictions. Further, as expected, the IO had better performance, as measured by the receiver operating characteristic (ROC) curve, than the Hotelling observer. This method is developed for SPECT imaging. However, it can be adapted to any linear imaging system.

Fig. 1

Applying the MCMC IO estimation technique in the case where a parameterized phantom and simulated system are used.

Fig. 2

Parameterized torso phantom.

Fig. 3

An example of the definition of P_body (m̃−m).

Fig. 4

Segment of the Markov chain.

Fig. 5

Λ_BKE obtained (a) from the first 10 iterations, and (b) from the 11th to 30th iterations. Note that vertical scale is different for (a) and (b).

Fig. 6

Λ_BKE evaluated at 40–4000 iterations. It can be seen that the Markov chain stabilizes after 1000 iterations.

Fig. 7

Convergence of Λ̂ for a particular data vector g⃑.

Fig. 8

Histogram of (a) Λ̅_block and (b) log Λ̅_block.

Fig. 9

The convergence of 〈Λ̂|H₀〉.

Fig. 10

The histogram of ideal observer likelihood ratios. The plot on the right expands the region indicated on the left by using 10 histogram bins (as opposed to two). In these plots, the points indicate the location of the histogram bin and the lines only represent a smooth curve drawn through the points.

Fig. 11

(a) Histograms of Hotelling observer test statistics. (b) Histograms of IO test statistic, log Λ̂, of the two classes.

Fig. 12

The convergence of 〈Λ̂|H₁〉 − Var(Λ̂|H₀).

Fig. 13

ROC curves of the two observers. The ROC curve of IO is uniformly better than that of the HO.

Fig. 14

Plot of M₀(β) as a function of β. The curve has the expected quadratic shape and passes very close to the point (1.0, 1.0) at the right endpoint.