Minimal folding pathways for coarse-grained biopolymer fragments
- PMID: 18820236
- PMCID: PMC2599856
- DOI: 10.1529/biophysj.108.135046
Minimal folding pathways for coarse-grained biopolymer fragments
Abstract
The minimal folding pathway or trajectory for a biopolymer can be defined as the transformation that minimizes the total distance traveled between a folded and an unfolded structure. This involves generalizing the usual Euclidean distance from points to one-dimensional objects such as a polymer. We apply this distance here to find minimal folding pathways for several candidate protein fragments, including the helix, the beta-hairpin, and a nonplanar structure where chain noncrossing is important. Comparing the distances traveled with root mean-squared distance and mean root-squared distance, we show that chain noncrossing can have large effects on the kinetic proximity of apparently similar conformations. Structures that are aligned to the beta-hairpin by minimizing mean root-squared distance, a quantity that closely approximates the true distance for long chains, show globally different orientation than structures aligned by minimizing root mean-squared distance.
Figures


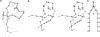
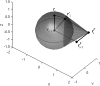

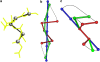
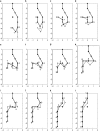

References
-
- Klimov, D. K., and D. Thirumalai. 1998. Lattice models for proteins reveal multiple folding nuclei for nucleation-collapse mechanism. J. Mol. Biol. 282:471–492. - PubMed
-
- Ozkan, S. B., K. A. Dill, and I. Bahar. 2003. Computing the transition state populations in simple protein models. Biopolymers. 68:35–46. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources

