Role of NADH/NAD+ transport activity and glycogen store on skeletal muscle energy metabolism during exercise: in silico studies
- PMID: 18829894
- PMCID: PMC2636997
- DOI: 10.1152/ajpcell.00094.2008
Role of NADH/NAD+ transport activity and glycogen store on skeletal muscle energy metabolism during exercise: in silico studies
Abstract
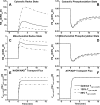
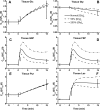
Skeletal muscle can maintain ATP concentration constant during the transition from rest to exercise, whereas metabolic reaction rates may increase substantially. Among the key regulatory factors of skeletal muscle energy metabolism during exercise, the dynamics of cytosolic and mitochondrial NADH and NAD+ have not been characterized. To quantify these regulatory factors, we have developed a physiologically based computational model of skeletal muscle energy metabolism. This model integrates transport and reaction fluxes in distinct capillary, cytosolic, and mitochondrial domains and investigates the roles of mitochondrial NADH/NAD+ transport (shuttling) activity and muscle glycogen concentration (stores) during moderate intensity exercise (60% maximal O2 consumption). The underlying hypothesis is that the cytosolic redox state (NADH/NAD+) is much more sensitive to a metabolic disturbance in contracting skeletal muscle than the mitochondrial redox state. This hypothesis was tested by simulating the dynamic metabolic responses of skeletal muscle to exercise while altering the transport rate of reducing equivalents (NADH and NAD+) between cytosol and mitochondria and muscle glycogen stores. Simulations with optimal parameter estimates showed good agreement with the available experimental data from muscle biopsies in human subjects. Compared with these simulations, a 20% increase (or approximately 20% decrease) in mitochondrial NADH/NAD+ shuttling activity led to an approximately 70% decrease (or approximately 3-fold increase) in cytosolic redox state and an approximately 35% decrease (or approximately 25% increase) in muscle lactate level. Doubling (or halving) muscle glycogen concentration resulted in an approximately 50% increase (or approximately 35% decrease) in cytosolic redox state and an approximately 30% increase (or approximately 25% decrease) in muscle lactate concentration. In both cases, changes in mitochondrial redox state were minimal. In conclusion, the model simulations of exercise response are consistent with the hypothesis that mitochondrial NADH/NAD+ shuttling activity and muscle glycogen stores affect primarily the cytosolic redox state. Furthermore, muscle lactate production is regulated primarily by the cytosolic redox state.
Figures







Similar articles
-
NAD(+)/NADH and skeletal muscle mitochondrial adaptations to exercise.Am J Physiol Endocrinol Metab. 2012 Aug 1;303(3):E308-21. doi: 10.1152/ajpendo.00054.2012. Epub 2012 Mar 20. Am J Physiol Endocrinol Metab. 2012. PMID: 22436696 Free PMC article. Review.
-
Regulation of lactate production at the onset of ischaemia is independent of mitochondrial NADH/NAD+: insights from in silico studies.J Physiol. 2005 Dec 15;569(Pt 3):925-37. doi: 10.1113/jphysiol.2005.093146. Epub 2005 Oct 13. J Physiol. 2005. PMID: 16223766 Free PMC article.
-
Role of O2 in regulation of lactate dynamics during hypoxia: mathematical model and analysis.Ann Biomed Eng. 1998 Jan-Feb;26(1):1-27. doi: 10.1114/1.28. Ann Biomed Eng. 1998. PMID: 10355547
-
Metabolic dynamics in skeletal muscle during acute reduction in blood flow and oxygen supply to mitochondria: in-silico studies using a multi-scale, top-down integrated model.PLoS One. 2008 Sep 9;3(9):e3168. doi: 10.1371/journal.pone.0003168. PLoS One. 2008. PMID: 18779864 Free PMC article.
-
The redox switch/redox coupling hypothesis.Neurochem Int. 2006 May-Jun;48(6-7):523-30. doi: 10.1016/j.neuint.2005.12.036. Epub 2006 Mar 10. Neurochem Int. 2006. PMID: 16530294 Review.
Cited by
-
The effect of exercise-intensity on skeletal muscle stress kinase and insulin protein signaling.PLoS One. 2017 Feb 9;12(2):e0171613. doi: 10.1371/journal.pone.0171613. eCollection 2017. PLoS One. 2017. PMID: 28182793 Free PMC article. Clinical Trial.
-
'Idealized' state 4 and state 3 in mitochondria vs. rest and work in skeletal muscle.PLoS One. 2015 Feb 3;10(2):e0117145. doi: 10.1371/journal.pone.0117145. eCollection 2015. PLoS One. 2015. PMID: 25647747 Free PMC article.
-
A need for NAD+ in muscle development, homeostasis, and aging.Skelet Muscle. 2018 Mar 7;8(1):9. doi: 10.1186/s13395-018-0154-1. Skelet Muscle. 2018. PMID: 29514713 Free PMC article. Review.
-
Exercise-induced metabolic fluctuations influence AMPK, p38-MAPK and CaMKII phosphorylation in human skeletal muscle.Physiol Rep. 2015 Sep;3(9):e12462. doi: 10.14814/phy2.12462. Physiol Rep. 2015. PMID: 26359238 Free PMC article.
-
NAD(+)/NADH and skeletal muscle mitochondrial adaptations to exercise.Am J Physiol Endocrinol Metab. 2012 Aug 1;303(3):E308-21. doi: 10.1152/ajpendo.00054.2012. Epub 2012 Mar 20. Am J Physiol Endocrinol Metab. 2012. PMID: 22436696 Free PMC article. Review.
References
-
- Ainscow EK, Brand MD. Top-down control analysis of ATP turnover, glycolysis and oxidative phosphorylation in rat hepatocytes. Eur J Biochem 263: 671–685, 1999. - PubMed
-
- Alberty RA Calculation of standard transformed Gibbs energies and standard transformed enthalpies of biochemical reactants. Arch Biochem Biophys 353: 116–130, 1998. - PubMed
-
- Alberty RA Thermodynamics of Biochemical Reactions. Hoboken, NJ: John Wiley & Sons, 2003.
-
- Balaban RS Regulation of oxidative phosphorylation in the mammalian cell. Am J Physiol Cell Physiol 258: C377–C389, 1990. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Medical

