Biomechanical ordering of dense cell populations

Abstract

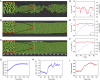
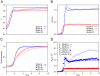
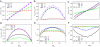
The structure of bacterial populations is governed by the interplay of many physical and biological factors, ranging from properties of surrounding aqueous media and substrates to cell-cell communication and gene expression in individual cells. The biomechanical interactions arising from the growth and division of individual cells in confined environments are ubiquitous, yet little work has focused on this fundamental aspect of colony formation. We analyze the spatial organization of Escherichia coli growing in a microfluidic chemostat. We find that growth and expansion of a dense colony of cells leads to a dynamical transition from an isotropic disordered phase to a nematic phase characterized by orientational alignment of rod-like cells. We develop a continuum model of collective cell dynamics based on equations for local cell density, velocity, and the tensor order parameter. We use this model and discrete element simulations to elucidate the mechanism of cell ordering and quantify the relationship between the dynamics of cell proliferation and the spatial structure of the population.

Fig. 1.

Experimental results for bacterial growth and ordering from an evenly distributed low-density seeding of cells. (A–C) Three snapshots of E. coli monolayer growth and ordering in a quasi-2D open microfluidic cavity taken at 60, 90, and 138 min from the beginning of the experiment. (D–F) Velocity and density profiles along the channel corresponding to the snapshots to the left. (G–I) Time traces of mean density, velocity gradient, and order parameter.

Fig. 2.

Comparison of continuum and DES modeling of the bacterial growth. Shown are time traces of the amplitudes of density (A), velocity gradient (B), order parameter (C), and stress components for constant growth rate (D) (A = 2.0; models A and C1) and pressure-dependent growth rate (A = 4.0; models B and C2). Results of the continuum modeling are indicated by lines, and results of the DES simulations are indicated by symbols. Parameters of continuum models A and B are: L = 1, P = 10, s = 0.4, ρ_c^d = 0.62, ρ_c⁰ = 0.7, B = 1, μ = 8, α₀ = 1, p_c = 1.6.

Fig. 3.

DES of the ordering dynamics in channels with different aspect ratios. (A) Orientation of individual cells (color-coded) in the system with A = 2.0 and a constant growth rate (model C1). (B) Velocity field for the same case as in A, where unit velocity vectors show the velocity direction for each cell and colors (from blue to red) correspond to the velocity magnitude (from low to high). (C) The same as A, but for a twice longer system (A = 4.0). Defects of the orientation are constantly created in the middle of the channel and advected by the flow toward the open boundaries. (D) The same as B, but for a twice longer system (A = 4.0). The flow is no longer laminar, and there is no apparent correlation between orientation and velocity magnitude.

Fig. 4.

DES of bacterial growth for the pressure-independent growth condition (model C1) in channels with different aspect ratios, varying in the range A = 2–4. For each aspect ratio, we show the time evolution of the total number of cells within the channel (A), the pressure in the middle of the channel (B), the mean velocity gradient (C), and the averaged order parameter (D). (D Inset) The decay of the asymptotic value of the order parameter with the aspect ratio, A. Time is measured in units of the inverse growth rate.

Fig. 5.

Spatiotemporal dynamics of bacterial growth generated by using DES. (A and B) Evolution of profiles of velocity and pressure along the channel in the short system (A = 2). (C–F) Stationary profiles of the velocity, pressure, density, and order parameter for channels of different aspect ratios: A = 2, 3, 4 for the case of constant growth rate (model C1) and A = 4 for the case of pressure-dependent growth rate (model C2).