A genetic timer through noise-induced stabilization of an unstable state
- PMID: 18836072
- PMCID: PMC2560995
- DOI: 10.1073/pnas.0806349105
A genetic timer through noise-induced stabilization of an unstable state
Abstract
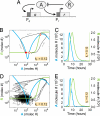
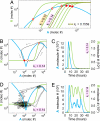
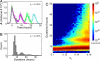
Stochastic fluctuations affect the dynamics of biological systems. Typically, such noise causes perturbations that can permit genetic circuits to escape stable states, triggering, for example, phenotypic switching. In contrast, studies have shown that noise can surprisingly also generate new states, which exist solely in the presence of fluctuations. In those instances noise is supplied externally to the dynamical system. Here, we present a mechanism in which noise intrinsic to a simple genetic circuit effectively stabilizes a deterministically unstable state. Furthermore, this noise-induced stabilization represents a unique mechanism for a genetic timer. Specifically, we analyzed the effect of noise intrinsic to a prototypical two-component gene-circuit architecture composed of interacting positive and negative feedback loops. Genetic circuits with this topology are common in biology and typically regulate cell cycles and circadian clocks. These systems can undergo a variety of bifurcations in response to parameter changes. Simulations show that near one such bifurcation, noise induces oscillations around an unstable spiral point and thus effectively stabilizes this unstable fixed point. Because of the periodicity of these oscillations, the lifetime of the noise-dependent stabilization exhibits a polymodal distribution with multiple, well defined, and regularly spaced peaks. Therefore, the noise-induced stabilization presented here constitutes a minimal mechanism for a genetic circuit to function as a timer that could be used in the engineering of synthetic circuits.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
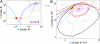
Similar articles
-
Dynamics of the interlocked positive feedback loops explaining the robust epigenetic switching in Candida albicans.J Theor Biol. 2009 May 7;258(1):71-88. doi: 10.1016/j.jtbi.2009.01.008. Epub 2009 Jan 24. J Theor Biol. 2009. PMID: 19490874
-
Delays induce novel stochastic effects in negative feedback gene circuits.Biophys J. 2014 Jan 21;106(2):467-78. doi: 10.1016/j.bpj.2013.12.010. Biophys J. 2014. PMID: 24461022 Free PMC article.
-
Switching between oscillations and homeostasis in competing negative and positive feedback motifs.J Theor Biol. 2012 Aug 21;307:205-10. doi: 10.1016/j.jtbi.2012.04.011. Epub 2012 Apr 21. J Theor Biol. 2012. PMID: 22762992
-
Build to understand: synthetic approaches to biology.Integr Biol (Camb). 2016 Apr 18;8(4):394-408. doi: 10.1039/c5ib00252d. Epub 2015 Dec 21. Integr Biol (Camb). 2016. PMID: 26686885 Free PMC article. Review.
-
Stochastic models for circadian rhythms: effect of molecular noise on periodic and chaotic behaviour.C R Biol. 2003 Feb;326(2):189-203. doi: 10.1016/s1631-0691(03)00016-7. C R Biol. 2003. PMID: 12754937 Review.
Cited by
-
Computing with biological switches and clocks.Nat Comput. 2018;17(4):761-779. doi: 10.1007/s11047-018-9686-x. Epub 2018 Jun 1. Nat Comput. 2018. PMID: 30524215 Free PMC article.
-
Genetic Redundancies Enhance Information Transfer in Noisy Regulatory Circuits.PLoS Comput Biol. 2016 Oct 14;12(10):e1005156. doi: 10.1371/journal.pcbi.1005156. eCollection 2016 Oct. PLoS Comput Biol. 2016. PMID: 27741249 Free PMC article.
-
Synaptic mechanisms for motor variability in a feedforward network.Sci Adv. 2020 Jun 19;6(25):eaba4856. doi: 10.1126/sciadv.aba4856. Print 2020 Jun. Sci Adv. 2020. PMID: 32937495 Free PMC article.
-
The role of feedback control mechanisms on the establishment of oscillatory regimes in the Ras/cAMP/PKA pathway in S. cerevisiae.EURASIP J Bioinform Syst Biol. 2012 Jul 20;2012(1):10. doi: 10.1186/1687-4153-2012-10. EURASIP J Bioinform Syst Biol. 2012. PMID: 22818197 Free PMC article.
-
Effects of cell cycle noise on excitable gene circuits.Phys Biol. 2016 Nov 30;13(6):066007. doi: 10.1088/1478-3975/13/6/066007. Phys Biol. 2016. PMID: 27902489 Free PMC article.
References
-
- Bar-Even A, et al. Noise in protein expression scales with natural protein abundance. Nat Genet. 2006;38(6):636–643. - PubMed
-
- Blake WJ, et al. Noise in eukaryotic gene expression. Nature. 2003;422(6932):633–637. - PubMed
-
- Elowitz MB, et al. Stochastic gene expression in a single cell. Science. 2002;297(5584):1183–1186. - PubMed
-
- Newman JR, et al. Single-cell proteomic analysis of S. cerevisiae reveals the architecture of biological noise. Nature. 2006;441(7095):840–846. - PubMed
-
- Ozbudak EM, et al. Regulation of noise in the expression of a single gene. Nat Genet. 2002;31(1):69–73. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

