Computational approaches to spatial orientation: from transfer functions to dynamic Bayesian inference

Abstract

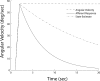
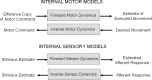
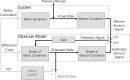
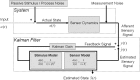
Spatial orientation is the sense of body orientation and self-motion relative to the stationary environment, fundamental to normal waking behavior and control of everyday motor actions including eye movements, postural control, and locomotion. The brain achieves spatial orientation by integrating visual, vestibular, and somatosensory signals. Over the past years, considerable progress has been made toward understanding how these signals are processed by the brain using multiple computational approaches that include frequency domain analysis, the concept of internal models, observer theory, Bayesian theory, and Kalman filtering. Here we put these approaches in context by examining the specific questions that can be addressed by each technique and some of the scientific insights that have resulted. We conclude with a recent application of particle filtering, a probabilistic simulation technique that aims to generate the most likely state estimates by incorporating internal models of sensor dynamics and physical laws and noise associated with sensory processing as well as prior knowledge or experience. In this framework, priors for low angular velocity and linear acceleration can explain the phenomena of velocity storage and frequency segregation, both of which have been modeled previously using arbitrary low-pass filtering. How Kalman and particle filters may be implemented by the brain is an emerging field. Unlike past neurophysiological research that has aimed to characterize mean responses of single neurons, investigations of dynamic Bayesian inference should attempt to characterize population activities that constitute probabilistic representations of sensory and prior information.

FIG. 1.

Schematic illustration of velocity storage. For a constant velocity stimulus (- - -), the angular velocity estimate of the CNS (-·-·-) outlasts the angular velocity signaled by the afferent signals from the semicircular canals (—).

FIG. 2.

Examples of internal models for sensory and motor processing.

FIG. 3.

Traditional observer model architecture (after Merfeld et al. 1993). The observer functions by comparing the output and the estimated output to generate a feedback signal that is passed through an internal model of motor dynamics to generate the state estimate. The state estimate, in turn, is passed through the model of sensor dynamics to generate the estimated output, which is used to generate a feedback signal, and so on. For passive observers, the input, u(t), is set to 0, motor dynamics are not relevant (i.e., set to unity transfer), and there is no comparison between estimated and desired states to generate a control signal (omit gray lines). Passive observers are suited to modeling passive perception.

FIG. 4.

Kalman filter model (after Borah et al. 1988). A simplified version is depicted to illustrate how the Kalman filter approach parallels the Observer model in Fig. 3. The model resembles a passive observer, so input is set to 0, and motor dynamics (not shown) are set to unity transfer. The feedback signal is multiplied by the statistically optimal Kalman gain. The result is passed through the internal model of the system dynamics, which includes the stimulus internal model and the internal model of sensor dynamics. Note that the Kalman filter uses the state space representation of these internal models.

FIG. 5.

In a Kalman filter model, the time constant of the angular velocity estimate (velocity storage) depends on 2 parameters: the SD of the Gaussian-distributed noise on the canal signal (σ_v) and the bandwidth cutoff of stimulus internal model (β). Values of canal noise increase from left to right from 5 to 20°/s. Values for the bandwidth cutoff increase from top to bottom. The red dashed lines indicate the actual angular velocity, the gray lines show the estimated angular velocity, and the blue lines show the mean of that estimate during each second of the simulation. A 1st-order approximation of the transfer function proposed by Borah et al. (1988) was used; this does not affect behavior of the model for the frequencies of stimulation examined here.

FIG. 6.

In a particle filter model, the time constant of the angular velocity estimate (velocity storage) also depends on 2 parameters: the noise in the canal signal (σ_V) and the variability of the angular velocity prior (σ_Ω). The red dashed line illustrates the actual angular velocity and the blue lines show the time course of the angular velocity estimate. Values of canal noise (σ_V) increase on the columns from left to right from 5 to 20°/s. Values for prior variability (σ_Ω) increase on the rows from bottom to top from 15 to 60°/s. The time constant for velocity storage depends (approximately) on the ratio between σ_V and σ_Ω. The grayscale represents the variability associated with the estimate.

FIG. B1.

The Kalman filter is implemented by the internal model parameters A–C and the computed Kalman gain L_k.