Modelling heterotachy in phylogenetic inference by reversible-jump Markov chain Monte Carlo

Abstract

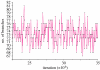
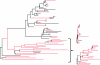
The rate at which a given site in a gene sequence alignment evolves over time may vary. This phenomenon--known as heterotachy--can bias or distort phylogenetic trees inferred from models of sequence evolution that assume rates of evolution are constant. Here, we describe a phylogenetic mixture model designed to accommodate heterotachy. The method sums the likelihood of the data at each site over more than one set of branch lengths on the same tree topology. A branch-length set that is best for one site may differ from the branch-length set that is best for some other site, thereby allowing different sites to have different rates of change throughout the tree. Because rate variation may not be present in all branches, we use a reversible-jump Markov chain Monte Carlo algorithm to identify those branches in which reliable amounts of heterotachy occur. We implement the method in combination with our 'pattern-heterogeneity' mixture model, applying it to simulated data and five published datasets. We find that complex evolutionary signals of heterotachy are routinely present over and above variation in the rate or pattern of evolution across sites, that the reversible-jump method requires far fewer parameters than conventional mixture models to describe it, and serves to identify the regions of the tree in which heterotachy is most pronounced. The reversible-jump procedure also removes the need for a posteriori tests of 'significance' such as the Akaike or Bayesian information criterion tests, or Bayes factors. Heterotachy has important consequences for the correct reconstruction of phylogenies as well as for tests of hypotheses that rely on accurate branch-length information. These include molecular clocks, analyses of tempo and mode of evolution, comparative studies and ancestral state reconstruction. The model is available from the authors' website, and can be used for the analysis of both nucleotide and morphological data.

Figure 1

Growth in the use of molecular phylogenies in scientific research. Source: Web of Science, April, 2008. Search terms molecular AND phylogen^*. Line of best fit is a quadratic spline. Dashed lines indicate that period doubling time is increasing.

Figure 2

Random topology of 70 taxa with branch lengths corresponding to branch-length set 1 drawn on the uniform interval 0–0.2. Inset: scatterplot of branch lengths from set 1 versus branch lengths from set 2.

Figure 3

Time-series plot taken from a segment of the converged Markov chain of the posterior distribution of extra branches derived from the reversible-jump algorithm. Mean=73±2.5.

Figure 4

The posterior probability of the reversible-jump algorithm identifying two branches as a function of the absolute difference in the true lengths of the two branches. P₅₀ denotes the point on the x-axis (0.040, red circle) where there is a 50% chance of detecting a second branch. S-shaped curve is a two-parameter logistic model.

Figure 5

The phylogeny of the Gnetales (table 1). The tree is derived as a consensus of the posterior sample of trees produced by the reversible-jump mixture model. For edges with more than one branch length, the consensus length is the weighted mean of the lengths for that edge. Colours identify edges with a greater than 50% chance of having two distinct lengths in the posterior sample. Inset shows the two sets of branch lengths for the clade with pronounced heterotachy.