Bayesian analysis of amino acid substitution models

Abstract

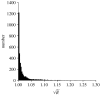
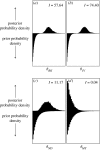
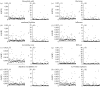
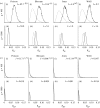
Models of amino acid substitution present challenges beyond those often faced with the analysis of DNA sequences. The alignments of amino acid sequences are often small, whereas the number of parameters to be estimated is potentially large when compared with the number of free parameters for nucleotide substitution models. Most approaches to the analysis of amino acid alignments have focused on the use of fixed amino acid models in which all of the potentially free parameters are fixed to values estimated from a large number of sequences. Often, these fixed amino acid models are specific to a gene or taxonomic group (e.g. the Mtmam model, which has parameters that are specific to mammalian mitochondrial gene sequences). Although the fixed amino acid models succeed in reducing the number of free parameters to be estimated--indeed, they reduce the number of free parameters from approximately 200 to 0--it is possible that none of the currently available fixed amino acid models is appropriate for a specific alignment. Here, we present four approaches to the analysis of amino acid sequences. First, we explore the use of a general time reversible model of amino acid substitution using a Dirichlet prior probability distribution on the 190 exchangeability parameters. Second, we then explore the behaviour of prior probability distributions that are'centred' on the rates specified by the fixed amino acid model. Third, we consider a mixture of fixed amino acid models. Finally, we consider constraints on the exchangeability parameters as partitions,similar to how nucleotide substitution models are specified, and place a Dirichlet process prior model on all the possible partitioning schemes.

Figure 1

A frequency histogram of the potential scale reduction statistics $\left(\sqrt{\hat{R}}\right)$ for the parameters examined in this study.

Figure 2

The marginal prior and posterior probability distribution for four of the exchangeability parameters for the HIV pol alignment. The Kullback–Leibler divergence, I, is shown for each parameter and measures the dissimilarity between the prior and posterior probability distributions. Note that the Kullback–Leibler divergence is small for the M↔Y parameter where the prior and posterior distributions are similar. The data are more informative for the other parameters shown, and the Kullback–Leibler divergence is correspondingly larger.

Figure 3

The mean of the marginal posterior probability distribution [$[E(\theta |\mathit{X})]$] and the Kullback–Leibler divergence (I) for the 190 exchangeability parameters for each of the eight alignments examined in this study. The 190 exchangeability parameters are ordered along the x-axes.

Figure 4

The prior (dashed line) and posterior (solid line) marginal probability density for two of the 190 exchangeability parameters for analyses of the HIV alignment. The y-axis is the marginal posterior probability density of the rate.

Figure 5

The Kullback–Leibler divergences (y-axes) of the 190 exchangeability parameters (arranged along the x-axes) under four different centred prior distributions for the HIV alignment.

Figure 6

The marginal posterior probability distribution of the I↔V exchangeability parameter for the HIV alignment when Χ varies. The y-axis is the marginal posterior probability density of the rate. Red line, 0.1; blue line, 1; light green line, 100; orange line, 190; light blue line, 500; green line, 1000; yellow line, 10 000.

Figure 7

The prior and posterior probability distributions (upside down and right side up, respectively) for the number of exchangeability parameter groups for the analyses where the concentration parameter is fixed such that the prior mean of the number of substitution categories is 2 (i.e. E(K)=2). (a) Drosophila adh; (b) vertebrate β-globin; (c) Leviviridae coat; (d) Japanese encephalitis env; (e) flavivirus; (f) influenza; (g) HIV pol and (h) Leviviridae replicase.

Figure 8

The mean partitions of the exchangeability parameters for each of the analyses. For each alignment, three mean partitions are shown, with the top most having a prior mean of 2 and the bottom most having a prior mean of 10.