Robust simplifications of multiscale biochemical networks
- PMID: 18854041
- PMCID: PMC2654786
- DOI: 10.1186/1752-0509-2-86
Robust simplifications of multiscale biochemical networks
Abstract
Background: Cellular processes such as metabolism, decision making in development and differentiation, signalling, etc., can be modeled as large networks of biochemical reactions. In order to understand the functioning of these systems, there is a strong need for general model reduction techniques allowing to simplify models without loosing their main properties. In systems biology we also need to compare models or to couple them as parts of larger models. In these situations reduction to a common level of complexity is needed.
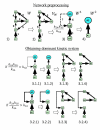
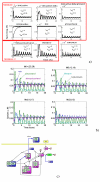
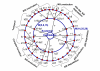
Results: We propose a systematic treatment of model reduction of multiscale biochemical networks. First, we consider linear kinetic models, which appear as "pseudo-monomolecular" subsystems of multiscale nonlinear reaction networks. For such linear models, we propose a reduction algorithm which is based on a generalized theory of the limiting step that we have developed in 1. Second, for non-linear systems we develop an algorithm based on dominant solutions of quasi-stationarity equations. For oscillating systems, quasi-stationarity and averaging are combined to eliminate time scales much faster and much slower than the period of the oscillations. In all cases, we obtain robust simplifications and also identify the critical parameters of the model. The methods are demonstrated for simple examples and for a more complex model of NF-kappaB pathway.
Conclusion: Our approach allows critical parameter identification and produces hierarchies of models. Hierarchical modeling is important in "middle-out" approaches when there is need to zoom in and out several levels of complexity. Critical parameter identification is an important issue in systems biology with potential applications to biological control and therapeutics. Our approach also deals naturally with the presence of multiple time scales, which is a general property of systems biology models.
Figures
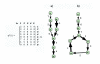


References
-
- Gorban AN, Radulescu O. Dynamic and static limitation in reaction networks, revisited. Advances in Chemical Engineering. 2008;34:103–173. http://arxiv.org/abs/physics/0703278
-
- Lam SH, Goussis DA. The CSP Method for Simplifying Kinetics. International Journal of Chemical Kinetics. 1994;26:461–486.
-
- Chiavazzo E, Gorban AN, Karlin IV. Comparisons of Invariant Manifolds for Model Reduction in Chemical Kinetics. Comm Comp Phys. 2007;2:964–992.
-
- Gorban AN, Karlin IV. Method of invariant manifold for chemical kinetics. Chem Eng Sci. 2003;58:4751–4768. doi: 10.1016/j.ces.2002.12.001. - DOI
-
- Gorban AN, Karlin IV. Invariant manifolds for physical and chemical kinetics, Lect Notes Phys 660. Berlin, Heidelberg: Springer; 2005.
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Molecular Biology Databases

