An end to endless forms: epistasis, phenotype distribution bias, and nonuniform evolution
- PMID: 18949026
- PMCID: PMC2562988
- DOI: 10.1371/journal.pcbi.1000202
An end to endless forms: epistasis, phenotype distribution bias, and nonuniform evolution
Abstract
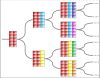
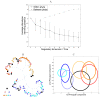
Studies of the evolution of development characterize the way in which gene regulatory dynamics during ontogeny constructs and channels phenotypic variation. These studies have identified a number of evolutionary regularities: (1) phenotypes occupy only a small subspace of possible phenotypes, (2) the influence of mutation is not uniform and is often canalized, and (3) a great deal of morphological variation evolved early in the history of multicellular life. An important implication of these studies is that diversity is largely the outcome of the evolution of gene regulation rather than the emergence of new, structural genes. Using a simple model that considers a generic property of developmental maps-the interaction between multiple genetic elements and the nonlinearity of gene interaction in shaping phenotypic traits-we are able to recover many of these empirical regularities. We show that visible phenotypes represent only a small fraction of possibilities. Epistasis ensures that phenotypes are highly clustered in morphospace and that the most frequent phenotypes are the most similar. We perform phylogenetic analyses on an evolving, developmental model and find that species become more alike through time, whereas higher-level grades have a tendency to diverge. Ancestral phenotypes, produced by early developmental programs with a low level of gene interaction, are found to span a significantly greater volume of the total phenotypic space than derived taxa. We suggest that early and late evolution have a different character that we classify into micro- and macroevolutionary configurations. These findings complement the view of development as a key component in the production of endless forms and highlight the crucial role of development in constraining biotic diversity and evolutionary trajectories.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
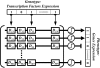

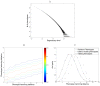

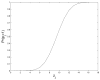
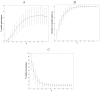
 ,
r = 18.
,
r = 18.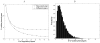

References
-
- de Visser J, Hermisson J, Wagner G, Ancel Meyers L, Bagheri-Chaichian H, et al. Evolution and detection of genetic robustness. Evolution. 2003;57:1959–1972. - PubMed
-
- Fontana W, Schuster P. Shaping space: the possible and the attainable in RNA genotype-phenotype mapping. J Theor Biol. 1998;194:491–515. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

