Unexpected power-law stress relaxation of entangled ring polymers

Abstract

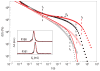
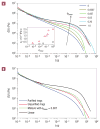
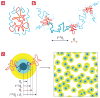
After many years of intense research, most aspects of the motion of entangled polymers have been understood. Long linear and branched polymers have a characteristic entanglement plateau and their stress relaxes by chain reptation or branch retraction, respectively. In both mechanisms, the presence of chain ends is essential. But how do entangled polymers without ends relax their stress? Using properly purified high-molar-mass ring polymers, we demonstrate that these materials exhibit self-similar dynamics, yielding a power-law stress relaxation. However, trace amounts of linear chains at a concentration almost two decades below their overlap cause an enhanced mechanical response. An entanglement plateau is recovered at higher concentrations of linear chains. These results constitute an important step towards solving an outstanding problem of polymer science and are useful for manipulating properties of materials ranging from DNA to polycarbonate. They also provide possible directions for tuning the rheology of entangled polymers.

Figure 1. Illustration of entangled polymer conformations and relaxation models

a, Reptation of linear chain. Topological constraints due to neighbours (black dots) force the chain to carry out snake-like motion along its contour (brighter colours show earlier conformations). b, Relaxation of star by arm retraction. Diffusion is possible only if arms are completely retracted and pushed around the constraints. c, A double-folded ring reptating through uncrossable obstacles. d, A double-folded ring optimizing its conformational entropy in an array of fixed obstacles^–. The red bullets illustrate a gate (constraints formed by obstacles). The orange loop has to be pulled out of it (see text). e, The shape of this ring can be mapped onto a ‘lattice animal’ structure, exhibiting self-similarity in hierarchy of relaxation: the ring relaxes from outermost towards inner sections. f, Mutual penetration of rings increases conformational entropy by opening-up double folds, while simultaneously blocking the gliding of the previously double-folded strands.

Figure 2. Stress relaxation moduli G(t) of entangled polymers

Comparison of the data (T_ref = 170 °C) for two polystyrene rings (R198: open triangles and R161: open squares) with the model predictions (solid and dotted lines) of equation (1) and with their linear counterparts (respectively filled triangles and filled squares). The short straight dashed lines indicate the relaxation times τ_e and τ_d and the plateau modulus G_N of the linear chains (see text). Inset: Characterization of the purified ring polymers. SEC chromatograms of the rings before (mother samples; symbols) and after LCCC fractionation (lines), showing the fraction of the eluted polymer against its elution volume.

Figure 3. Effects of added linear chains on entangled purified ring polymer rheology

Data from mixtures of polystyrene rings with linear polymers of the same molar mass at different added fractions ϕ_linear. a, Stress relaxation modulus G(t) of the R198 mixtures at T_ref = 170 °C. Inset: Extrapolated zero-shear-rate viscosity of mixtures of purified ring and linear chains of the same molar mass, as a function of linear fraction. Data for mixtures with rings R198 (triangles) and R160 (squares) are shown. b, Comparison of the G(t) for the same ring R198 before (red line) and after (blue line) LCCC purification. The G(t) of the mixture with ϕ_linear = 0.007 (green line) and the respective linear melt (black line) are shown for comparison.

Figure 4. Illustrations of conformations of mixtures involving ring and linear polymers

a, Penetration of rings by linear chains in their mixture locally opens the double-folded ring structure. b, Multiple ring penetrations prevent rings from relaxing and bridge chains into an effective transient network. Dotted lines show relaxed chain sections up to the ring relaxation time. The root-mean-square end-to-end distance of the unrelaxed fraction f of a linear chain (bold blue line) is smaller than its root-mean-square end-to-end distance R_e by a factor of f^1/2. The distance between two opposite monomers in a compressed ring in a melt is R_r. c, Left: Geometric representation of characteristic sizes of rings and linear chains in b. Linear polymer radius of gyration is R_g. Right: Transient network of linear chains bridged by rings. Whereas linear chains (blue circles) are below their percolation threshold, when they are bridged by (yellow) rings the resulting structure percolates through the system, yielding enhanced mechanical response.