Understanding the evolution and stability of the G-matrix
- PMID: 18973631
- PMCID: PMC3229175
- DOI: 10.1111/j.1558-5646.2008.00472.x
Understanding the evolution and stability of the G-matrix
Abstract
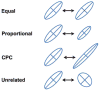
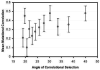
The G-matrix summarizes the inheritance of multiple, phenotypic traits. The stability and evolution of this matrix are important issues because they affect our ability to predict how the phenotypic traits evolve by selection and drift. Despite the centrality of these issues, comparative, experimental, and analytical approaches to understanding the stability and evolution of the G-matrix have met with limited success. Nevertheless, empirical studies often find that certain structural features of the matrix are remarkably constant, suggesting that persistent selection regimes or other factors promote stability. On the theoretical side, no one has been able to derive equations that would relate stability of the G-matrix to selection regimes, population size, migration, or to the details of genetic architecture. Recent simulation studies of evolving G-matrices offer solutions to some of these problems, as well as a deeper, synthetic understanding of both the G-matrix and adaptive radiations.
Figures






References
-
- Arnold SJ. Constraints on phenotypic evolution. Am Nat. 1992;140:S85–S107. - PubMed
-
- Arnold SJ, Phillips PC. Hierarchical comparison of genetic variance covariance matrices. II. Coastal-inland divergence in the garter snake, Thamnophis elegans. J Evol Biol. 1999;53:1516–1527. - PubMed
-
- Arnold SJ, Pfrender ME, Jones AG. Tire adaptive landscape as a conceptual bridge between micro- and macroevolution. Genetica. 2001:112–113. 9–32. - PubMed
-
- Baatz M, Wagner GP. Adaptive inertia caused by hidden pleiotropic effects. Theor Pop Biol. 1997;5:49–66.
-
- Barton N, Keightley PD. Understanding quantitative genetic variation. Nat Rev Genet. 2002;3:11–20. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous
