Accelerated failure time models provide a useful statistical framework for aging research

Abstract

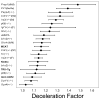
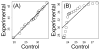
Survivorship experiments play a central role in aging research and are performed to evaluate whether interventions alter the rate of aging and increase lifespan. The accelerated failure time (AFT) model is seldom used to analyze survivorship data, but offers a potentially useful statistical approach that is based upon the survival curve rather than the hazard function. In this study, AFT models were used to analyze data from 16 survivorship experiments that evaluated the effects of one or more genetic manipulations on mouse lifespan. Most genetic manipulations were found to have a multiplicative effect on survivorship that is independent of age and well-characterized by the AFT model "deceleration factor". AFT model deceleration factors also provided a more intuitive measure of treatment effect than the hazard ratio, and were robust to departures from modeling assumptions. Age-dependent treatment effects, when present, were investigated using quantile regression modeling. These results provide an informative and quantitative summary of survivorship data associated with currently known long-lived mouse models. In addition, from the standpoint of aging research, these statistical approaches have appealing properties and provide valuable tools for the analysis of survivorship data.

Figure 1

Survivorship curves from control and experimental treatments. Part (A) shows survivorship curves associated with control cohorts from the 18 comparisons listed in Table 1. Part (B) shows survivorship curves associated with (long-lived) experimental cohorts from the 22 comparisons listed in Table 1.

Figure 2

AFT model deceleration factor estimates. The deceleration factor represents the parameter c in the relation S₁ (ct) = S₀ (t), where S₁ (t) is the survivorship of the experimental cohort at time t and S₀ (t) represents survivorship of the control cohort at time t (Equation 1). The value of 100(c − 1) provides an estimate of the percent treatment difference in lifespan (experimental versus control) for any survival time quantile. For each comparison (see Table 1), filled symbols indicate the estimated deceleration factor value and bars represent a 95% confidence interval. Some deceleration factor estimates have been adjusted for covariates such as parental IDs, date of birth or gender (see Table 2).

Figure 3

Quantile-Quantile plots. Survival time quantiles calculated from control cohort survival times are plotted against corresponding survival time quantiles calculated from experimental cohort survival times. Part (A) shows a QQ plot for the Pit1(dw/dw) comparison and part (B) shows a QQ plot for the Clk1(+/−)(S2) comparison. The solid line represents a least-square regression line. Part (A) indicates that the AFT model appropriately describes the treatment effect for the Pit1(dw/dw) comparison, since points approximate a straight line. Part (B) suggests that the AFT model may not be appropriate for the Clk1(+/−)(S2) comparison, since points do not approximate a straight line. QQ plots for all 22 Table 1 comparisons are shown in Supplemental Data File 1.

Figure 4

Deceleration factors estimates and control cohort lifespan. The plot shows a weak positive association between deceleration factor estimates and median lifespan estimates from control cohorts. Each point represents one of the 22 comparisons listed in Table 1.

Figure 5

Log-cumulative hazard plots. Part (A) shows a log-cumulative hazard plot for the Prop1(df/df) comparison, while part (B) shows the log-cumulative hazard plot for the Surf1(−/−) comparison. In both (A) and (B), the dotted line represents the logarithm of the estimated hazard function for the experimental treatment, while the solid line represents the logarithm of the estimated hazard function for the control treatment. Part (A) shows that, for the Prop1(df/df) comparison, the difference between log-hazard functions of control and experimental treatments is roughly consistent over time (as assumed by the PH model). Part (B) shows that, for the Surf1(−/−) comparison, the difference between log-hazard functions of control and experimental treatments varies over time, which suggests that the standard PH model may not be appropriate. Log-cumulative hazard plots for each of the 22 Table 1 comparisons are shown in Supplemental Data File 3.

Figure 6

Quantile regression estimation of treatment effects. Quantile regression was used to estimate treatment effects across a range of survival time quantiles (τ = 0.10,…,0.90). For a given quantile τ (horizontal axis), the vertical axis represents the percent increase in survivorship associated with an experimental treatment (Koenker and Geling, 2001). In part (A), results for the PappA(−/−) treatment are shown, and in part (B), results for the bIrs2(+/−) treatment are shown. In each plot, the middle line represents the calculated effect of experimental treatments at each survival time quantile, while the upper and lower lines outline a 95% confidence region (Koenker and Geling, 2001).