Regularized positive-definite fourth order tensor field estimation from DW-MRI

Abstract

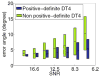
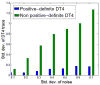
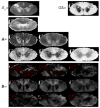
In Diffusion Weighted Magnetic Resonance Image (DW-MRI) processing, a 2nd order tensor has been commonly used to approximate the diffusivity function at each lattice point of the DW-MRI data. From this tensor approximation, one can compute useful scalar quantities (e.g. anisotropy, mean diffusivity) which have been clinically used for monitoring encephalopathy, sclerosis, ischemia and other brain disorders. It is now well known that this 2nd-order tensor approximation fails to capture complex local tissue structures, e.g. crossing fibers, and as a result, the scalar quantities derived from these tensors are grossly inaccurate at such locations. In this paper we employ a 4th order symmetric positive-definite (SPD) tensor approximation to represent the diffusivity function and present a novel technique to estimate these tensors from the DW-MRI data guaranteeing the SPD property. Several articles have been reported in literature on higher order tensor approximations of the diffusivity function but none of them guarantee the positivity of the estimates, which is a fundamental constraint since negative values of the diffusivity are not meaningful. In this paper we represent the 4th-order tensors as ternary quartics and then apply Hilbert's theorem on ternary quartics along with the Iwasawa parametrization to guarantee an SPD 4th-order tensor approximation from the DW-MRI data. The performance of this model is depicted on synthetic data as well as real DW-MRIs from a set of excised control and injured rat spinal cords, showing accurate estimation of scalar quantities such as generalized anisotropy and trace as well as fiber orientations.

Fig. 1

Comparison of the fiber orientation errors for different amounts of noise in the data, obtained by using: a) our parametrization to enforce positivity and b) without enforcing positivity of the estimated tensors.

Fig. 2

Comparison of the standard deviation of the generalized trace [13], obtained by using: a) our parametrization that enforces positivity and b) without enforcing positivity of the estimated tensors.

Fig. 3

Illustration of the advantage of the proposed parametrization, against the non unique parametrization in [1]. In this example we regularized a noisy R synthetic tensor field by minimizing ∫|| ∇ C_x || dx, where C_x are the parameters of each parametrization, and x is the lattice index.

Fig. 4

Fiber orientation errors for different SNR in the data using our method for the estimation of positive 4^th-order tensors and two other existing methods: 1) DOT and 2) ODF.

Fig. 5

The elements of matrices A and B estimated by the proposed method as well the estimated S₀ and generalized anisotropy [13].

Fig. 6

4^th-order tensors estimated without imposing the SPD property (left) and by using the proposed method (right). On the top the corresponding estimated S₀ images are shown colored by mapping the X, Y, Z coordinates of the largest diffusivity orientation to the R, G, B color components. In this region of interest we expected single-lobed diffusivities with peaks predominantly in the axial direction (shown in blue).

Fig. 7

Visualization of the 4^th-order tensor field estimated by applying proposed method to a real DW-MRI dataset from an excised rat’s spinal cord.

Fig. 8

The acquired S₀ image of a control (left) and three injured rat spinalcords.

Fig. 9

Comparison of the fiber orientations estimated in the control and the corresponding registered injured cord dataset. The S₀ images are shown on the top of the figure.

Fig. 10

Visualization of the ROI (shown in pink) in 3D. The plots show comparisons between the fiber orientation angle of the average diffusivity in the ROI and the histogram of variances in the ROI.

Fig. 11

Quantitative comparison of the rat spinal cord dataset using the Rie-mannian metric of the 15 × 15 positive definite matrices. The Riemannian distances between the covariance matrices are shown on the left. The corresponding hierarchical dendrogram computed using the Riemannian distances.