Statistical mechanics and the evolution of polygenic quantitative traits
- PMID: 19087953
- PMCID: PMC2651070
- DOI: 10.1534/genetics.108.099309
Statistical mechanics and the evolution of polygenic quantitative traits
Abstract
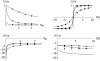
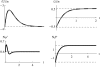
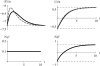
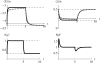
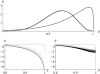
The evolution of quantitative characters depends on the frequencies of the alleles involved, yet these frequencies cannot usually be measured. Previous groups have proposed an approximation to the dynamics of quantitative traits, based on an analogy with statistical mechanics. We present a modified version of that approach, which makes the analogy more precise and applies quite generally to describe the evolution of allele frequencies. We calculate explicitly how the macroscopic quantities (i.e., quantities that depend on the quantitative trait) depend on evolutionary forces, in a way that is independent of the microscopic details. We first show that the stationary distribution of allele frequencies under drift, selection, and mutation maximizes a certain measure of entropy, subject to constraints on the expectation of observable quantities. We then approximate the dynamical changes in these expectations, assuming that the distribution of allele frequencies always maximizes entropy, conditional on the expected values. When applied to directional selection on an additive trait, this gives a very good approximation to the evolution of the trait mean and the genetic variance, when the number of mutations per generation is sufficiently high (4Nmicro > 1). We show how the method can be modified for small mutation rates (4Nmicro --> 0). We outline how this method describes epistatic interactions as, for example, with stabilizing selection.
Figures
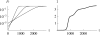

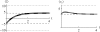

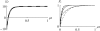
References
-
- Barton, N. H., 1986. The maintenance of polygenic variation through a balance between mutation and stabilizing selection. Genet. Res. 49 157–174. - PubMed
-
- Barton, N. H., 1989. The divergence of a polygenic system under stabilizing selection, mutation and drift. Genet. Res. 54 59–77. - PubMed
-
- Barton, N. H., and P. D. Keightley, 2002. Understanding quantitative genetic variation. Nat. Rev. Genet. 3 11–21. - PubMed
-
- Barton, N. H., and M. Turelli, 1987. Adaptive landscapes, genetic distance, and the evolution of quantitative characters. Genet. Res. 49 157–174. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

