Stochastic dynamics and non-equilibrium thermodynamics of a bistable chemical system: the Schlögl model revisited
- PMID: 19095615
- PMCID: PMC2838355
- DOI: 10.1098/rsif.2008.0476
Stochastic dynamics and non-equilibrium thermodynamics of a bistable chemical system: the Schlögl model revisited
Abstract
Schlögl's model is the canonical example of a chemical reaction system that exhibits bistability. Because the biological examples of bistability and switching behaviour are increasingly numerous, this paper presents an integrated deterministic, stochastic and thermodynamic analysis of the model. After a brief review of the deterministic and stochastic modelling frameworks, the concepts of chemical and mathematical detailed balances are discussed and non-equilibrium conditions are shown to be necessary for bistability. Thermodynamic quantities such as the flux, chemical potential and entropy production rate are defined and compared across the two models. In the bistable region, the stochastic model exhibits an exchange of the global stability between the two stable states under changes in the pump parameters and volume size. The stochastic entropy production rate shows a sharp transition that mirrors this exchange. A new hybrid model that includes continuous diffusion and discrete jumps is suggested to deal with the multiscale dynamics of the bistable system. Accurate approximations of the exponentially small eigenvalue associated with the time scale of this switching and the full time-dependent solution are calculated using Matlab. A breakdown of previously known asymptotic approximations on small volume scales is observed through comparison with these and Monte Carlo results. Finally, in the appendix section is an illustration of how the diffusion approximation of the chemical master equation can fail to represent correctly the mesoscopically interesting steady-state behaviour of the system.
Figures



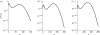



 and right FCA
and right FCA  . The lines have been darkened when the FCA is more stable to illustrate that the entropy production rate decreases as the height of the more stable barrier increases. The parameter values used are k1=3, k2=0.6, k3=0.25, k4=2.95, b=0.5 and 0.9≤a≤2.4. The point at which the FCA exchange stability is a=1.105, is indicated by the intersection of the bold and dashed lines. Grey dashed line,
. The lines have been darkened when the FCA is more stable to illustrate that the entropy production rate decreases as the height of the more stable barrier increases. The parameter values used are k1=3, k2=0.6, k3=0.25, k4=2.95, b=0.5 and 0.9≤a≤2.4. The point at which the FCA exchange stability is a=1.105, is indicated by the intersection of the bold and dashed lines. Grey dashed line,  when n
− is less stable; grey solid line,
when n
− is less stable; grey solid line,  when n
+ is less stable; black dashed line,
when n
+ is less stable; black dashed line,  when n
− is more stable; black solid line,
when n
− is more stable; black solid line,  when n
+ is more stable.
when n
+ is more stable.

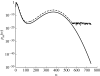
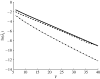

 to the asymptotic predictions Δu
± as V increases.
to the asymptotic predictions Δu
± as V increases.Similar articles
-
Non-Equilibrium Thermodynamics and Stochastic Dynamics of a Bistable Catalytic Surface Reaction.Entropy (Basel). 2018 Oct 23;20(11):811. doi: 10.3390/e20110811. Entropy (Basel). 2018. PMID: 33266535 Free PMC article.
-
Bistability: requirements on cell-volume, protein diffusion, and thermodynamics.PLoS One. 2015 Apr 15;10(4):e0121681. doi: 10.1371/journal.pone.0121681. eCollection 2015. PLoS One. 2015. PMID: 25874711 Free PMC article.
-
Temperature-driven coherence resonance and stochastic resonance in a thermochemical system.Phys Rev E Stat Nonlin Soft Matter Phys. 2014 Feb;89(2):022916. doi: 10.1103/PhysRevE.89.022916. Epub 2014 Feb 18. Phys Rev E Stat Nonlin Soft Matter Phys. 2014. PMID: 25353554
-
The chemical master equation approach to nonequilibrium steady-state of open biochemical systems: linear single-molecule enzyme kinetics and nonlinear biochemical reaction networks.Int J Mol Sci. 2010 Sep 20;11(9):3472-500. doi: 10.3390/ijms11093472. Int J Mol Sci. 2010. PMID: 20957107 Free PMC article. Review.
-
Driving rapidly while remaining in control: classical shortcuts from Hamiltonian to stochastic dynamics.Rep Prog Phys. 2023 Jan 10;86(3). doi: 10.1088/1361-6633/acacad. Rep Prog Phys. 2023. PMID: 36535018 Review.
Cited by
-
Operant conditioning of stochastic chemical reaction networks.PLoS Comput Biol. 2022 Nov 18;18(11):e1010676. doi: 10.1371/journal.pcbi.1010676. eCollection 2022 Nov. PLoS Comput Biol. 2022. PMID: 36399506 Free PMC article.
-
Stochastic E2F activation and reconciliation of phenomenological cell-cycle models.PLoS Biol. 2010 Sep 21;8(9):e1000488. doi: 10.1371/journal.pbio.1000488. PLoS Biol. 2010. PMID: 20877711 Free PMC article.
-
The limiting dynamics of a bistable molecular switch with and without noise.J Math Biol. 2016 Aug;73(2):367-95. doi: 10.1007/s00285-015-0949-1. Epub 2015 Dec 21. J Math Biol. 2016. PMID: 26692266
-
Processes on the emergent landscapes of biochemical reaction networks and heterogeneous cell population dynamics: differentiation in living matters.J R Soc Interface. 2017 May;14(130):20170097. doi: 10.1098/rsif.2017.0097. J R Soc Interface. 2017. PMID: 28490602 Free PMC article. Review.
-
Foraging Dynamics and Entropy Production in a Simulated Proto-Cell.Entropy (Basel). 2022 Dec 8;24(12):1793. doi: 10.3390/e24121793. Entropy (Basel). 2022. PMID: 36554198 Free PMC article.
References
-
- Andresen B., Zimmermann E. C., Ross J. 1984. Objections to a proposal on the rate of entropy production in systems far from equilibrium. J. Chem. Phys. 81, 4676–4677.10.1063/1.447402 - DOI
-
- Andrieux D., Gaspard P. 2007. Fluctuation theorem for currents and Schnakenberg network theory. J. Stat. Phys. 127, 107–131.10.1007/s10955-006-9233-5 - DOI
-
- Baras F., Mansour M. M. 1997. Particle simulations of chemical systems. Adv. Chem. Phys. 100, 393–474.
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources

