Dependence of bacterial chemotaxis on gradient shape and adaptation rate

Abstract

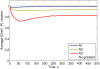
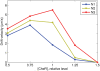
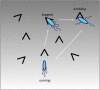
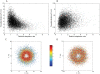
Simulation of cellular behavior on multiple scales requires models that are sufficiently detailed to capture central intracellular processes but at the same time enable the simulation of entire cell populations in a computationally cheap way. In this paper we present RapidCell, a hybrid model of chemotactic Escherichia coli that combines the Monod-Wyman-Changeux signal processing by mixed chemoreceptor clusters, the adaptation dynamics described by ordinary differential equations, and a detailed model of cell tumbling. Our model dramatically reduces computational costs and allows the highly efficient simulation of E. coli chemotaxis. We use the model to investigate chemotaxis in different gradients, and suggest a new, constant-activity type of gradient to systematically study chemotactic behavior of virtual bacteria. Using the unique properties of this gradient, we show that optimal chemotaxis is observed in a narrow range of CheA kinase activity, where concentration of the response regulator CheY-P falls into the operating range of flagellar motors. Our simulations also confirm that the CheB phosphorylation feedback improves chemotactic efficiency by shifting the average CheY-P concentration to fit the motor operating range. Our results suggest that in liquid media the variability in adaptation times among cells may be evolutionary favorable to ensure coexistence of subpopulations that will be optimally tactic in different gradients. However, in a porous medium (agar) such variability appears to be less important, because agar structure poses mainly negative selection against subpopulations with low levels of adaptation enzymes. RapidCell is available from the authors upon request.

Figure 1. Model of chemotactic E. coli.

(A) Scheme of the hybrid model. The activity of the receptor cluster depends on the local ligand concentration and the methylation level according to the MWC model. Methylation (red arrow) and demethylation (blue arrow) are performed by CheR and CheB. The phosphate group is transferred from active CheA to the response regulator CheY (black arrow). The concentration of CheY-P modulates the motor bias of 5 independent motors (yellow arrows), and their collective behavior makes the cell run or tumble. Ligand binding, receptors cluster switching, CheY phosphorylation and motor switching are considered to be in rapid equilibrium and are described by algebraic equations, while the methylation and demethylation kinetics are relatively slow and simulated using an ODE. Motor switching is simulated stochastically. (B) The model reproduces the swimming of E. coli cells up gradients of attractants, taking into account the effect of rotational diffusion. A typical path of a swimming virtual cell is shown in 2D space, with the relative time course shown along the Z axis, demonstrating how the cell finds the maximum attractant concentration and stays in its vicinity. The attractant concentration profile is overlayed.

Figure 2. Simulation of the MWC model response to the constant-activity and exponential ramps of aspartate.

(A) The concentration profiles of constant-activity and exponential ramps of aspartate, relative to K_D = 4.52 µM (logarithmic scale). (B) The response of the MWC model to the applied constant-activity and exponential ramps. Upon stimulation with the constant-activity ramp, the [CheY-P] rapidly goes down during initial excitation—the single non-smooth point on the slope is the result of the piece-wise linearity of the methylation energy function. The constant-activity ramp produces a long flat response up to a concentration of 100K_D, above which Tsr receptors become sensitive to the ligand and the cluster activity falls. Upon stimulation with the exponential ramp, the cell initially adapts to the minimum concentration C_min = 0.31K_D, and after 200 s the exponential ramp begins. After 700 s, adaptation overcomes excitation and [CheY-P] slowly returns to the steady state. Relative adaptation rate k = 1.

Figure 3. Simulations of chemotaxis in different gradients.

(A) Concentration profiles of the gradients used in the simulations. (B) Chemotactic drift of cells in these gradients. The average position 〈X〉 of the cells is shown as a function of time. A population of 2000 cells starts moving from the left wall (x ₀ = 10 µm, y ₀ randomly distributed in (0, y_max)), and swims for 2000 s. (C) Relative CheY-P concentration as a function of time, averaged over 2000 cells in the same gradients. The gray line indicates the fully adapted state [CheY-P] = 1.0 in a medium without attractant. Relative adaptation rate k = 1. All cellular parameters are as described in Table 1.

Figure 4. Average CheY-P levels of 5000 cells swimming in the constant-activity gradients N1 (blue), N2 (green) and N3 (red).

Relative adaptation rate k = 1. The cell parameters are as described in Table 1.

Figure 5. Chemotactic properties of cells at different adaptation rates in constant-activity gradients.

(A) Drift velocity of cells in the constant-activity gradient N2 as a function of adaptation rate. The horizontal axis shows the adaptation rate k relative to the wild type (logarithmic scale). Gray lines show standard deviations. (B) Maximal drift velocities (black) and the corresponding optimal adaptation rates (blue) as a function of gradient steepness. The steepness of the constant-activity gradients was changed over a 64-fold range, as described in the section ‘Model of the environment’.

Figure 6. Optimal chemotactic behavior at different adaptation rates.

(A) Drift velocities of cells as a function of adaptation rate, in the constant-activity gradients N1 (blue), N2 (green), N3 (red). For each adaptation rate, the drift velocity was estimated from the simulation of 1000 cells, with standard error of mean 0.05. (B) Average CheY-P levels of cells in the same simulations. Black dots indicate the adaptation rate at which drift velocity is maximal. Gray rectangles show the intervals of optimal adaptation rates, defined by taking the 90%-interval from the drift velocity maximum. The width of each rectangle indicates the optimal adaptation-rate interval, and height shows the corresponding CheY-P interval. All three intervals of adaptation rates fall into the same CheY-P interval: [0.80,0.97], shown by the gray band. (C) The CCW motor bias as a function of CheY-P. Gray bands indicate the optimal CheY-P interval and the corresponding operating range of the motor. The cell parameters are as described in Table 1.

Figure 7. Effect of variable [CheR] on chemotactic efficiency.

The vertical axis shows drift velocities. The level of [CheB] is fixed at the wild-type value (0.28 µM), while [CheR] is varied relative to wild type (0.16 µM). Note the steep fall in the drift velocities for [CheR]>1, where the steady-state CheY-P produces tumbling behavior.

Figure 8. Effect of CheB phosphorylation on chemotactic efficiency in a liquid medium.

(A) Drift velocity as a function of adaptation rate in the constant-activity gradients N1 (blue), N2 (green), N3 (red). The ratio of [CheR] to [CheB] at steady state is left as in the wild type (0.16/0.28), ensuring the steady-state activity A ^* = 1/3 in all cases. Solid lines correspond to cells with 100%-active CheB at steady state, dashed lines - 50%-active, finely dashed - 25%-active CheB. (B) The average [CheY-P] resulting from the balance between CheR and CheB activity determines the positive or negative role of CheB phosphorylation. Cells are simulated in the gradient N3, at adaptation rates of 1.0 and 3.0. Kinase-dependent CheB activity means that CheB works more weakly at A<1/3, and thus the average [CheY-P] is higher than the level obtained for constantly active CheB. Such a shift improves chemotaxis at low adaptation rates, but reduces it at high rates. The optimal range of CheY-P is shown by the gray band. (C) Drift velocities at variable [CheR] and variable CheB activity and fixed [CheB] (0.28 µM, wild type). Solid, dashed and finely dashed lines indicate 100%, 50% and 25% active CheB, respectively. Adaptation rate k = 1, other cell parameters as described in Table 1.

Figure 9. Model of motility in a porous medium (agar).

A cell encounters traps along its run, and stops in the traps. It stays in the trapped state until the first tumble occurs, then normal run and tumble behavior resumes. The trap positions are not fixed in the 2D space - instead, it is assumed that each cell encounters traps in a series of randomly distributed time intervals.

Figure 10. Swarm-plate assay at different [CheR,CheB].

(A) Experimentally measured chemotactic efficiency at different expression levels of the cheR cheB-eyfp operon under the control of a pBAD promoter. The applied arabinose concentrations were 0.0, 0.0005, 0.001, 0.01%, respectively. The CheB-YFP level reflects the concerted [CheR,CheB-YFP] due to strong translational coupling. For scale conversion, the wild-type level of CheB can be taken as 240 copies/cell . (B) Simulated chemotactic efficiency as a function of [CheR,CheB]. Cells are simulated in the constant-activity gradients N1 (blue), N2 (green), N3 (red). The black open circle shows the experimentally observed drift velocity of wild-type cells, estimated from Figure 4 of . The cross shows the drift velocity of non-adapting cells, from Figure 6 of . The cell parameters are as described in Table 1. (C) Average motor bias of cells as a function of [CheR,CheB]. The steady-state motor bias is 0.65, with the gray band indicating the region of optimal motor bias for chemotaxis in agar.

Figure 11. Simulation of motility in a liquid medium and agar with a physiological [CheR,CheB] distribution.

The distances R travelled by 10⁴ cells after 1000 s of simulation time in (A) the liquid medium, N2 gradient; (B) agar, N3 gradient. The (x,y)-positions of cells colored from deep blue to red, according to their [CheR,CheB], are shown in (C) for the liquid medium, (D) for agar. The smallest [CheR,CheB] values correspond to deep blue, the highest values correspond to red. Note the different scales of the figures. The cell parameters are as described in Table 1.

Figure 12. Experimental measurement of [CheR,CheB-YFP] in individual cells at different points in the swarm ring, for plates with (A) normal agar (0.27%); (B) liquid agar (0.20%).

Blue columns show the least swarming cells in the center of the swarm plate, and the red ones—the best swarming cells from the outer edge. The expression of cheR cheB-yfp was under the control of a pBAD promoter, which gives a basal expression level close to wild-type. The bin size is 110 copies/cell.