Exact and approximate Fourier rebinning of PET data from time-of-flight to non time-of-flight
- PMID: 19124956
- PMCID: PMC4608752
- DOI: 10.1088/0031-9155/54/3/001
Exact and approximate Fourier rebinning of PET data from time-of-flight to non time-of-flight
Abstract
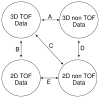
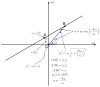
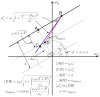
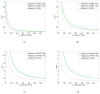
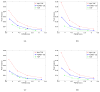
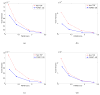
The image reconstruction problem for fully 3D TOF PET is challenging because of the large data sizes involved. One approach to this problem is to first rebin the data into one of the following lower dimensional formats: 2D TOF, 3D non TOF or 2D non TOF. Here we present a unified framework based on a generalized projection slice theorem for TOF data that can be used to compute each of these mappings. We use this framework to develop approaches for rebinning into non TOF formats without significant loss of information. We first derive the exact mappings and then describe approximations which address the missing data problem for oblique sinograms. We evaluate the performance of approximate rebinning using Monte Carlo simulations. Our results show that rebinning into non TOF sinograms retains significant SNR advantages over sinograms collected without TOF information.
Figures
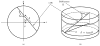




References
-
- Bai B, Smith AM. Fast 3D iterative reconstruction of PET images using PC graphics hardware. Proc IEEE Nuclear Science Symp Medical Imaging Conf. 2006:2787–90.
-
- Cho S, Li Q, Ahn S, Bai B, Leahy RM. Iterative image reconstruction using inverse Fourier rebinning for fully 3-D PET. IEEE Trans Med Imag. 2007;26(5):745–56. - PubMed
-
- Comtat C, Kinahan PE, Defrise M, Michel C, Townsend DW. Fast reconstruction of 3D PET data with accurate statistical modeling. IEEE Trans Nucl Sci. 1998;45(3):1083–9.
-
- De Man B, Basu S. Distance-driven projection and backprojection in three dimensions. Phys Med Biol. 2004;49:2463–75. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
