Spectral methods in machine learning and new strategies for very large datasets

Abstract

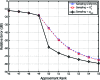
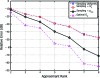
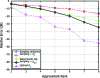
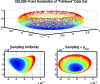
Spectral methods are of fundamental importance in statistics and machine learning, because they underlie algorithms from classical principal components analysis to more recent approaches that exploit manifold structure. In most cases, the core technical problem can be reduced to computing a low-rank approximation to a positive-definite kernel. For the growing number of applications dealing with very large or high-dimensional datasets, however, the optimal approximation afforded by an exact spectral decomposition is too costly, because its complexity scales as the cube of either the number of training examples or their dimensionality. Motivated by such applications, we present here 2 new algorithms for the approximation of positive-semidefinite kernels, together with error bounds that improve on results in the literature. We approach this problem by seeking to determine, in an efficient manner, the most informative subset of our data relative to the kernel approximation task at hand. This leads to two new strategies based on the Nyström method that are directly applicable to massive datasets. The first of these-based on sampling-leads to a randomized algorithm whereupon the kernel induces a probability distribution on its set of partitions, whereas the latter approach-based on sorting-provides for the selection of a partition in a deterministic way. We detail their numerical implementation and provide simulation results for a variety of representative problems in statistical data analysis, each of which demonstrates the improved performance of our approach relative to existing methods.

Fig. 1.

Relative approximation error of the randomized algorithms of Theorem 1 and as a function of approximant rank, shown relative to a baseline Nyström reconstruction obtained by sampling multi-indices uniformly at random.

Fig. 2.

Diffusion maps kernel approximation error as a function of approximant rank, shown for the 3 randomized algorithms of Fig. 1, along with the minimum approximation error attained by exact spectral decomposition.

Fig. 3.

Worst-case approximation error over 10 realizations of the random sampling schemes of Fig. 2, along with the deterministic algorithm of Theorem 2.

Fig. 4.

Recovery via Laplacian eigenmaps of a low-dimensional embedding from a 100,000-point realization of the “fishbowl” data set (Top), implemented using approximate spectral decompositions based on sampling multi-indices uniformly at random (Bottom Left) and according to the algorithm of Theorem 1 (Bottom Right).