Quantifying and correcting for the winner's curse in genetic association studies
- PMID: 19140131
- PMCID: PMC2706290
- DOI: 10.1002/gepi.20398
Quantifying and correcting for the winner's curse in genetic association studies
Abstract
Genetic association studies are a powerful tool to detect genetic variants that predispose to human disease. Once an associated variant is identified, investigators are also interested in estimating the effect of the identified variant on disease risk. Estimates of the genetic effect based on new association findings tend to be upwardly biased due to a phenomenon known as the "winner's curse." Overestimation of genetic effect size in initial studies may cause follow-up studies to be underpowered and so to fail. In this paper, we quantify the impact of the winner's curse on the allele frequency difference and odds ratio estimators for one- and two-stage case-control association studies. We then propose an ascertainment-corrected maximum likelihood method to reduce the bias of these estimators. We show that overestimation of the genetic effect by the uncorrected estimator decreases as the power of the association study increases and that the ascertainment-corrected method reduces absolute bias and mean square error unless power to detect association is high.
2009 Wiley-Liss, Inc.
Figures
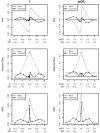
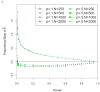

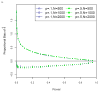

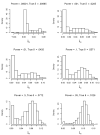
References
-
- Bazerman MH, Samuelson WF. I won the auction but don't want the prize. J Conflict Resolut. 1983;27:618–634.
-
- Carlin BP, Louis TA. Bayes and empirical Bayes methods for data analysis. 2nd. CRC Press; Boca Raton, FL: 2000.
-
- Garner C. Upward bias in odds ratio estimates from genome-wide association studies. Genet Epidemiol. 2007;31:288–295. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

