Periodic reversal of direction allows Myxobacteria to swarm

Abstract

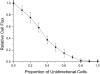
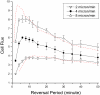
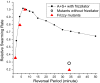
Many bacteria can rapidly traverse surfaces from which they are extracting nutrient for growth. They generate flat, spreading colonies, called swarms because they resemble swarms of insects. We seek to understand how members of any dense swarm spread efficiently while being able to perceive and interfere minimally with the motion of others. To this end, we investigate swarms of the myxobacterium, Myxococcus xanthus. Individual M. xanthus cells are elongated; they always move in the direction of their long axis; and they are in constant motion, repeatedly touching each other. Remarkably, they regularly reverse their gliding directions. We have constructed a detailed cell- and behavior-based computational model of M. xanthus swarming that allows the organization of cells to be computed. By using the model, we are able to show that reversals of gliding direction are essential for swarming and that reversals increase the outflow of cells across the edge of the swarm. Cells at the swarm edge gain maximum exposure to nutrient and oxygen. We also find that the reversal period predicted to maximize the outflow of cells is the same (within the errors of measurement) as the period observed in experiments with normal M. xanthus cells. This coincidence suggests that the circuit regulating reversals evolved to its current sensitivity under selection for growth achieved by swarming. Finally, we observe that, with time, reversals increase the cell alignment, and generate clusters of parallel cells.

Fig. 1.

Distribution of cells and multicellular structures at the swarm edge. In addition to some individual cells and slime trails, multicellular rafts and multicellular mounds are labeled. The swarm is expanding in the radial direction, which is to the right in this image. (Scale bar, 50μ.) This is the first frame of a 3 h time lapse movie (see Movie S1 in the SI).

Fig. 2.

Dependence of the flux on the proportion of unidirectional, wild-type cells. The average flux of 10 independent runs is plotted against the proportion of unidirectional cells in the mixture. Unidirectional cells were randomly distributed within the initial domain of cells, as described in Methods. A reversal period of 8 min was used for the reversing cells.

Fig. 3.

The average cell flux of 10 independent runs is shown with error bars that represent the standard deviation. Flux is plotted against the reversal periods for A⁺S⁺ bacteria and for an A⁺S⁻ mutant. The x-axis is scaled by log₁₀.

Fig. 4.

Dependence of the optimal reversal period on the cell speed. Simulation results for different speeds are presented for A⁺S⁺ cells. The red curves are reconstructed from the data of normal speed (4 μm/min), by using the functions Y = C1 * f(2x) for 8 μm/min and Y = C2 *f(x/2) for 2 μm/min respectively to show the effect of scale change. Here x is the reversal period, f(x) is the fitted function for the original curve of normal speed, and C1 and C2 are constant factors dependent on the average speed.

Fig. 5.

The orientational correlation functions for nonreversing cells and for reversal periods of 2, 8, and 50 min are plotted against the cell-cell distance for an A⁺S⁻ mutant after 400 min of simulation. The two curves in the inset are the orientation correlation functions calculated for wild-type and A⁺S⁻ cells outside the initial domain having an 8 min reversal period. The background level for the A⁺S⁻ (Inset) is smaller than the main figure because cells outside the initial domain have a lower density than cells at the very edge in the steady state. The correlation distances are shown by solid ovals. The cell–cell distance is given in units of cell length, where 1 cell length = 5 μm.

Fig. 6.

Dependence of the swarm expansion rate on the reversal period. Observed expansion rates for WT and 3 deletion frizzy mutants (red triangles) are compared with those computed from the model (all are relative values). Measurement of the swarm expansion rate is described in the SI.